분포 간의 거리를 측정하는 방법들
본 포스트에서는 생성 모델 GAN을 이해하기 위해 필요한 개념인 분포 간의 거리를 측정하는 방법들 KL divergence, JS divergence와 Wasserstein에 대해 정리해 보겠습니다. KL divergence는 우리가 분류 모델의 loss function으로 흔히 사용하는 Cross Entropy와 깊은 관계가 있습니다. KL divergence에 대해 알아보기 전에 Cross Entropy의 개념을 다시 한 번 짚어보겠습니다.
Cross Entropy
Cross Entropy는 주어진 실제 확률 분포와 모델이 예측한 확률 분포 간의 차이를 측정합니다. 주로 분류 문제에서 모델의 예측이 실제 라벨과 얼마나 일치하는지를 평가하는 데 사용됩니다. 이를 수식으로 표현하면 다음과 같습니다.
\[H(p,q)=- \sum_x p(x) \log q(x)\]여기에서 $p(x)$는 실제 분포의 확률이고, $q(x)$는 모델이 예측한 확률입니다.
Kullback-Leiver(KL) Divergence
KL divergence도 두 확률 분포 간의 차이를 측정하는 데 사용됩니다. 두 분포 $p$와 $q$가 주어졌을 때, $p$가 $q$를 통해 얼마나 잘 표현되는지를 측정합니다. KL Divergence는 상대적인 엔트로피(relative entropy)라고도 하는데요. 그 이유는 Cross Entropy로부터 KL Divergence를 유도하는 아래 수식을 보면 쉽게 이해할 수 있습니다.
\[\begin{align*}H(p,q) &= -\sum_x p(x) \log q(x) \\ &= -\sum_x p(x) \log q(x) - \sum_x p(x) \log p(x) + \sum_x p(x) \log p(x) \\ &= -\sum_x p(x) \log q(x) - H(p) + \sum_x p(x) \log p(x) \\ &= H(p) + \sum_x p(x) \log p(x) -\sum_x p(x) \log q(x) \\ &= H(p) + \sum_x p(x) \log \frac{p(x)}{q(x)}\end{align*}\]위 수식에서 $p$의 엔트로피 $H(p)$에 더해진 $\sum_x p(x) \log \frac{p(x)}{q(x)}$가 바로 KL Divergence입니다. 그리고 이를 다시 정리해 보면, 아래와 같이 cross entropy $H(p,q)$와 $p$의 엔트로피 $H(p)$의 차이로 표현할 수 있습니다.
\[\begin{align*}D_{KL}(p \lvert\rvert q) &= \sum_x p(x) \log \frac{p(x)}{q(x)} \\ &= H(p,q) - H(p)\end{align*}\]정보 이론의 정보량 관점에서 보면, KL divergence는 예측 분포 $q$가 실제 분포 $p$의 정보량을 얼마나 잘 보존하는지 측정하는 것입니다. KL divergence가 작을수록 $p$의 정보가 $q$로 변환될 때 손실이 적은 것이므로, 두 분포 간의 차이가 작다고 해석할 수 있습니다. 반면 KL divergence가 크다면 이는 $p$의 정보가 $q$로 변환될 때 많은 손실이 발생한다는 것을 의미하므로 $p$와 $q$는 매우 다른 분포라고 볼 수 있습니다.
KL divergence는 다음과 같은 두 가지 특징이 있습니다.
- $p$와 $q$가 모든 point에서 같을 때 최솟값 0을 갖습니다.
- 비대칭적(asymmetric)인 특징이 있어, $p$가 0에 가깝고 $q$는 0이 아닐 때 $q$ 효과는 무시됩니다. 따라서 동등하게 중요한 두 분포 사이의 유사도를 측정하고 싶을 때 적합하지 않습니다.
Jensen-Shannon(JS) Divergence
GAN 이전의 대표적인 생성 모델들 중 하나인 VAE는 loss function으로 KL divergence을 사용했는데요. GAN은 JS divergence를 사용합니다. Huszar, 2015에서는 GAN이 성공한 요인 중 하나가 loss function을 KL divergence에서 JS divergence로 바꾸었기 때문이라고 주장하기도 했을만큼, JS divergence은 GAN을 이해하기 위해 핵심적인 개념입니다. 먼저 GAN의 모델 구조를 간단히 되짚어보겠습니다.
Generative Adversarial Networks (GANs)
GAN은 생성기 $G$와 판별기 $D$로 구성되어 있습니다. 생성기는 실제 데이터의 분포 $p_{data}$를 모방하는 것을 목표로 하며, 판별기는 실제 데이터와 생성기가 생성한 가짜 데이터를 구별하려고 합니다. 판별기의 output은 Fake(0)와 Real(1) 사이의 확률값입니다. 이들의 상호작용은 아래와 같은 minimax 게임으로 표현됩니다.
\[\underset{G}{\min}\,\underset{D}{\max}\,V(D, G)=E_{x \sim p_{data}(x)}[\log D(x)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]\]여기서 $z$는 생성기의 입력인 잠재 변수를 의미합니다.
KL divergence와 JS divergence 비교
JS divergence는 두 분포 $p$과 $q$가 주어졌을 때, 두 분포의 중간 지점과의 차이를 측정합니다. JS divergence을 유도하는 과정은 아래와 같습니다.
- Assume $X$ an abstract function on the events, or a mixture distribution, $M$, with a mode selection of $Z$; and with two mode components of $p$ and $q$
- $X$ samples from $p$ distribution if $Z=0$
- $X$ samples from $q$ distribution if $Z=1$
- The mode proportion between $Z=0$ and $Z=1$ is uniform
- $X \sim M=\frac{p+q}{2}$
- 이 때, information gain은 $X$가 어느 분포로부터 샘플링되었는지 모를 때의 entropy와 $Z$를 알고 있을 때의 entropy의 차이로 정의할 수 있음
앞서 설명한 KL divergence와 비교해보면 아래와 같습니다.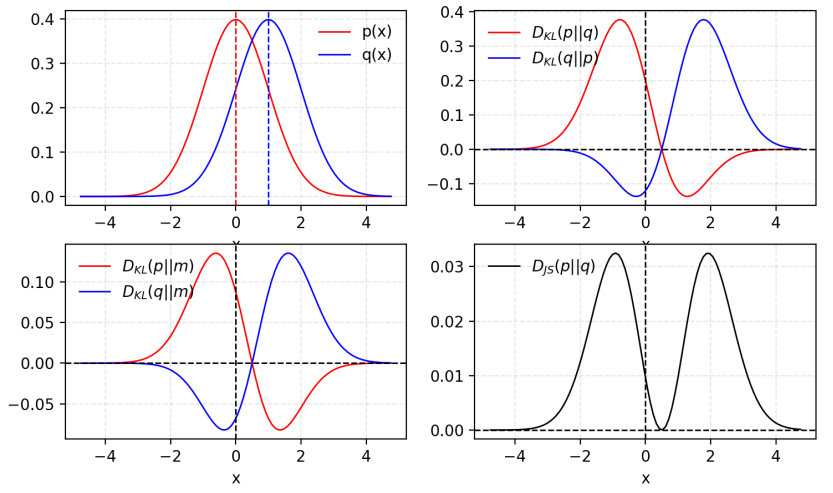 
KL divergence와 JS divergence 비교
- 두 분포의 중간 지점과 각 분포의 차이를 측정하므로, KL divergence처럼 무한대로 발산할 수 없음. [0, 1] 범위로 한정됨
- KL divergence보다 부드러움
- KL divergence와 달리 JS divergence는 대칭(symmetric)
JS Divergence와 GANs
다음으로, GAN의 loss function과 JS divergence의 관계에 대해 알아보겠습니다.
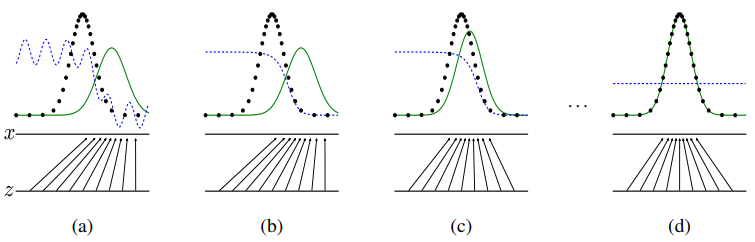
위 그림은 GAN이 학습되는 과정을 보여줍니다. 검정 점선은 실제 분포 $p_{data}$, 초록 실선은 가짜 분포 $p_{g}$, 파란 점선은 판별기의 분류 결과를 나타냅니다. (a) 학습 초기에는 판별기가 충분한 학습을 하지 못해서 주어진 이미지의 진위 여부를 불안정하게 예측합니다. 어느 정도 학습이 진행되면, (b) 판별기가 실제 데이터와 가짜 데이터를 잘 분류할 수 있게 되고, (c) 생성기도 학습 초기보다는 실제 데이터와 유사한 이미지를 생성합니다. (b)와 (c)가 반복되며 학습이 진행되다가 (d) 최종적으로 가짜 이미지의 분포가 실제 이미지의 분포와 동일해지면($p_{g}=p_{data}$) 판별기가 두 분포를 구분하지 못하고, 모든 데이터 포인트 $x$에서 0.5를 출력하게 됩니다($D(x)=0.5$).
위와 같은 학습을 가능하게 하는 loss function은 아래와 같습니다. 판별기는 아래 식을 최대화하고자 하고, 생성기는 최소화하고자 합니다.
\[\underset{G}{\min}\,\underset{D}{\max}\,V(D, G)=E_{x \sim p_{data}(x)}[\log D(x)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]\]이 loss function을 최대화하는 최적의 판별기 $D_G^*=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$이고, 이를 증명하면 다음과 같습니다.
\[\begin{align*}V(G,D) &= \int_x p_{data}(x) \log(D(x))dx + \int_z p_{z}(z) \log(1-D(g(x)))dz \\ &= \int_x p_{data}(x) \log(D(x)) + p_{g}(x) \log(1-D(x))dx\end{align*}\]위 식은 $a \log y + b \log(1-y)$ 형태이므로 $y=\frac{a}{a+b}$일 때 최댓값을 갖습니다. 따라서 최적의 판별기 $D^\ast(x)$는 $\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$입니다.
최적의 판별기 $D^\ast(x)$를 loss function에 대입해보면 아래와 같습니다.
\[\begin{align*}C(G) &= \underset{D}{\max}V(G,D) \\ &= E_{x \sim p_{data}(x)}[\log D^*(x)]+E_{z \sim p_{z}(z)}[\log (1-D^*(G(z)))] \\ &= E_{x \sim p_{data}(x)}[\log D^*(x)]+E_{x \sim p_{g}(x)}[\log (1-D^*(x))] \\ &= E_{x \sim p_{data}(x)}[\log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]+E_{x \sim p_{g}(x)}[\log \frac{p_{g}(x)}{p_{data}(x)+p_g(x)}]\end{align*}\]$C(G)$의 global minimum은 오직 $p_{g}=p_{data}$일 때 달성되며, 그 최솟값은 $- \log 4$입니다. 이를 증명하면 다음과 같습니다.
\[\begin{align*}C(G) &= E_{x \sim p_{data}(x)}[\log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]+E_{x \sim p_{g}(x)}[\log \frac{p_{g}(x)}{p_{data}(x)+p_g(x)}] \\ &= \sum p_{data}(x) \log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)} + \sum p_g(x) \log \frac{p_{g}(x)}{p_{data}(x)+p_g(x)} \\ &= -\log4 + \log4 + \sum p_{data}(x) \log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)} + \sum p_g(x) \log \frac{p_{g}(x)}{p_{data}(x)+p_g(x)} \\ &= -\log4 + \sum p_{data}(x) \log \frac{p_{data}(x)}{\frac{1}{2} \cdot \{ p_{data}(x)+p_g(x) \}} + \sum p_g(x) \log \frac{p_{g}(x)}{\frac{1}{2} \cdot \{ p_{data}(x)+p_g(x) \}} \\ &= -\log4 + D_{KL}(p_{data} \lvert\rvert \frac{p_{data}(x)+{p_g(x)}}{2}) + D_{KL}(p_{g} \lvert\rvert \frac{p_{data}(x)+{p_g(x)}}{2}) \\ &= -\log4 + 2 \cdot D_{JS}(p_{data} \lvert\rvert p_g)\end{align*}\]생성기가 위 식을 최소화하려면 두 분포 $p_{g}$, $p_{data}$의 JS divergence가 0이 되어야 합니다. 즉, 판별기가 구분할 수 없을 정도로 실제 데이터와 동일한 가짜 데이터를 만들어 JS divergence를 최소화해야 loss function을 최소화할 수 있습니다. 따라서 $C(G)$는 $p_{g}=p_{data}$일 경우에만 최솟값 $- \log 4$를 갖습니다. 그리고 이 때 $D^\ast(x) = \frac{p_{data}}{p_{data}+p_z}= 0.5$가 되어 모든 데이터 포인트 $x$에서 0.5를 출력하게 됩니다. 판별기가 실제 데이터와 가짜 데이터를 구분하지 못하게 되는 것입니다.
Wasserstein 거리 (Earth mover’s distance)
loss function을 JS divergence로 대체해도 GAN을 학습시키는 것은 여전히 어려운 문제입니다. 판별기와 생성기가 서로 반대의 목표를 가지고 있어 loss function이 수렴하기 어렵기 때문인데요. 이러한 문제를 해결하기 위해 JS divergence 대신 Wasserstein 거리를 사용하는 WGAN이 등장했습니다.
Wasserstein 거리의 정의
Wasserstein 거리는 두 분포 $p_{data}$, $p_g$를 비교할 때, 그 분포들을 구성하는 질량을 한 곳에서 다른 곳으로 옮기는 데 필요한 최소 이동 비용을 측정하는 방법입니다. WGAN에서는 두 이미지의 픽셀 값을 분포로 간주하여 한 이미지를 다른 이미지로 변환하는데 필요한 비용을 계산하는 데 사용됩니다. 즉, 생성된 이미지의 분포와 실제 이미지의 분포 사이의 차이를 계산하는 것입니다.
\[W_p(p_{data},p_g) = \left( \inf_{\gamma \in \Pi(p_{data},p_g)} \int_{\mathbb{R}^d \times \mathbb{R}^d} \|x - y\|^p \, d\gamma(x,y) \right)^{\frac{1}{p}}\]Wasserstein-1 거리는 위 수식에서 $p$가 1인 경우로, 수식은 다음과 같습니다.
\[\begin{align*} W_1(p_{data},p_g) &= \inf_{\gamma \in \Pi(p_{data},p_g)} \int_{\mathbb{R}^d \times \mathbb{R}^d} \|x - y\| \, d\gamma(x,y)\ \\ &= \inf_{\gamma \in \Pi(p_{data},p_g)} \mathbb{E}_{(x,y)\sim\gamma}[\|x - y\|] \end{align*}\]- $\Pi(P,Q)$: 분포 $P$와 $Q$사이에서 가능한 모든 결합 분포
- $\gamma(x,y)$: $\Pi(P,Q)$ 공간에 존재하는 결합 분포. $x$가 시작 지점, $y$가 도착 지점일 때, 이동한 전체 질량
- $\vert\vert x-y \vert\vert$: 공간 내의 두 점 $x$와 $y$ 사이의 거리
- $\inf$: 가능한 모든 결합 분포에 대해 최솟값을 찾는 연산
KL divergence와 JS divergence보다 좋은 지표인 이유
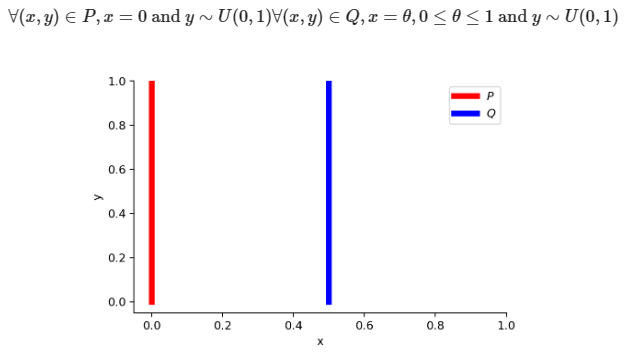
Wasserstein-1 거리는 두 분포의 형태가 다르거나 지지 집합(support)이 겹치지 않는 경우에도 거리를 측정할 수 있습니다. 예를 들어, 두 분포 $P$와 $Q$가 아래 그래프와 같을 때 KL divergence, JS divergence와 Wasserstein-1 거리는 다음과 같이 계산됩니다.
- KL divergence
- JS divergence
- Wasserstein 거리
$\theta$가 0이 아닐 때, 즉 두 분포가 서로 겹치지 않을 때 KL divergence는 무한대로 발산하여 의미있는 분포 간 차이를 산출할 수 없습니다. neural network의 loss function으로 사용될 때 gradient exploding 문제가 발생합니다. JS divergence는 무한대로 발산하지는 않지만, 최댓값 $\log2$를 가지며 이 때 gradient는 0이 됩니다. 이는 모델 최적화 과정에서 gradient vanishing 문제로 이어질 수 있습니다. KL divergence와 JS divergence는 모두 조건에 따라($\theta$에 따라) 그 값이 이산적(discrete)입니다. 반면, Wasserstein 거리는 $\theta$에 관계없이 $\vert \theta \vert$로, 부드러운 gradient signal을 제공함으로써 모델이 안정적으로 학습할 수 있도록 도와줍니다. 또한, KL divergence와 JS divergence과 달리 두 분포가 얼마나 멀리 떨어져 있는지($\theta$) 반영할 수 있다는 장점이 있습니다.