Kernel PCA

이번 포스트에서는 비선형 차원축소 기법 중 하나인 Kernel PCA에 대하여 알아보겠습니다. 이름에서 알 수 있듯이 Kernel trick과 PCA가 함께 사용되는 기법이기 때문에, 먼저 Kernel Trick과 PCA에 대한 이해가 필요한데요. PCA에 대한 설명은 이전 포스트을 참고하시면 됩니다.

Kernel Trick

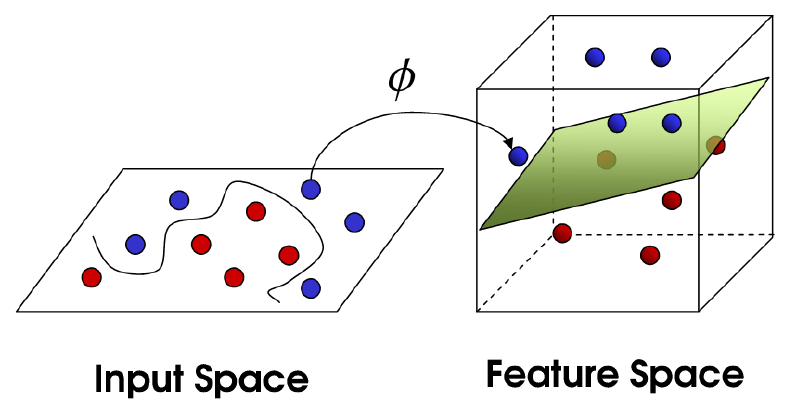
위 그림과 같이 input space에서 선형 분류가 불가능한 데이터를 mapping function $\phi$를 통해 고차원 공간(feature space)상에 mapping하면, 데이터를 선형 분류하는 hyperplane을 찾을 수 있습니다. 하지만 고차원 mapping은 많은 연산량이 소요된다는 문제가 있습니다. 이런 문제를 해결하면서, 고차원의 이점을 취하는 방법이 바로 Kernel Trick입니다.

kernel trick은 input space의 두 벡터 $x_i$, $x_j$를 받아서 고차원 상에서의 내적 값을 출력하는 kernel fucntion K를 찾습니다. 다시 말해 데이터를 고차원 상에 mapping하지 않고도 데이터를 고차원 상에 mapping한 것과 같은 효과를 얻는 것인데, 이를 수식으로 표현하면 다음과 같습니다. \(K(x_i,x_j)=\phi(x_i)^T\phi(x_i)\)

Kernel PCA

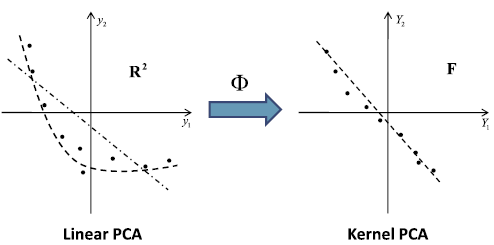
(출처) Kernel PCA의 핵심 아이디어는 비선형 kernel function $\phi$을 통해 데이터를 고차원 공간(F)에 mapping한 뒤, 고차원 공간(F)에서 PCA를 수행함으로써 다시 저차원 공간에 projection한다는 것입니다. Kernel PCA의 수행 과정을 수식으로 나타내면 다음과 같습니다.

먼저, 고차원 공간(feature space) 상에 mapping된 data point가 centering되어 있어 평균이 0이라고 가정합니다 \(m^\phi={1 \over N}\sum_{i=1}^N\phi(x_i)=0\)

이 데이터의 평균이 0이기 때문에, 공분산행렬 $C$를 구하면 다음과 같습니다.

\[C^\phi={1 \over N}\sum_{i=1}^N(\phi(x_i)-m^\phi)(\phi(x_i)-m^\phi)^T\\={1 \over N}\sum_{i=1}^N\phi(x_i)\phi(x_i)^T\]

공분산행렬 $C$의 eigenvalue $\lambda_k$와 eigenvector $v_k$는 다음과 같이 구할 수 있습니다.

\[C^\phi v_k=\lambda_k v_k\]

위 식에 공분산행렬 C의 값을 대입합니다.

\[{1 \over N}\sum_{i=1}^N\phi(x_i)\phi(x_i)^Tv_k=\lambda_k v_k\]

아래 식에서 $\phi(x_i)v_k$은 scalar이기 때문에 공분산행렬 C의 eigenvector $v_k$는 아래와 같이 고차원 상에 mapping된 data point들의 선형 결합으로 표현이 가능합니다.

\[v_k={1 \over \lambda N}\sum_{i=1}^N\phi(x_i)\phi(x_i)^Tv_k={1 \over \lambda N}\sum_{i=1}^N\phi(x_i)v_k\phi(x_i)^T\] \[=\sum_{i=1}^N\alpha_{ki}\phi(x_i)\] \[{1 \over N}\sum_{i=1}^N\phi(x_i)\phi(x_i)^T\sum_{j=1}^N\alpha_{kj}\phi(x_j)=\lambda_k \sum_{i=1}^N\alpha_{kj}\phi(x_i)\] \[{1 \over N}\sum_{i=1}^N\phi(x_i)\sum_{j=1}^N\alpha_{kj}\phi(x_i)^T\phi(x_j)=\lambda_k \sum_{i=1}^N\alpha_{kj}\phi(x_i)\]

앞서 Kernel Trick 파트에서 말씀드린 바와 같이, 고차원 mapping은 많은 연산량이 소요된다는 문제가 있기 때문에 Kernel PCA에서도 Kernel Trick을 사용하게 됩니다. 이를 위해 먼저 Kernel function을 정의합니다.

\[K(x_i,x_j)=\phi(x_i)^T\phi(x_j)\]

양 변에 $\phi(x_i)$을 곱하여 고차원 상에서의 data point들의 내적 값인 $\phi(x_i)^T\phi(x_j)$을 위에서 정의한 kernel function으로 치환합니다.

\[{1 \over N}\sum_{i=1}^N\phi(x_l)^T\phi(x_i)\sum_{j=1}^N\alpha_{kj}\phi(x_i)^T\phi(x_j)=\lambda_k \sum_{i=1}^N\alpha_{kj}\phi(x_l)^T\phi(x_i)\] \[{1 \over N}\sum_{i=1}^NK(x_l, x_i)\sum_{j=1}^N\alpha_{kj}K(x_i, x_l)=\lambda_k \sum_{i=1}^N\alpha_{kj}K(x_l, x_i)\]

위 식을 matirix notation을 이용하여 정리하면 다음과 같습니다.

\[K^2\alpha_k=\lambda_k N K \alpha_k\] \[K\alpha_k=\lambda_k N \alpha_k\]

따라서, Kernel PCA의 수행 결과는 다음과 같이 정리할 수 있습니다.

\[y_k(x)=\phi(x)^Tv_k=\sum_{i=1}^N\alpha_{ki}K(x,x_i)\]

지금까지의 진행 과정은 고차원 공간(feature space) 상에 mapping된 data point가 centering되어 있는 경우에 해당하는데요. data point가 centering되어 있지 않은 경우에는 아래와 같이 feature space에서 데이터를 표준화하는 과정을 거치게 됩니다. 아래 식에서 $1_N$은 모든 원소의 값이 $1 \over N$으로 이루어진 N X N 행렬을 의미합니다.

\[\tilde{K}=(I-1_N)K(I-1_N) \\ =K-1_NK-K1_N+1_NK1_N\]

Kernel PCA Using Python

여러 데이터 셋을 Kernel PCA와 Linear PCA에 적용해 보고 그 결과를 비교해 보았습니다. 코드는 이곳을 참고하였습니다.

Half-moon shapes

%matplotlib inline
import matplotlib.pyplot as plt

#하프문 데이터 생성
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, random_state=123)

plt.figure(figsize=(8,6))

plt.scatter(X[y==0, 0], X[y==0, 1], color='red', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', alpha=0.5)

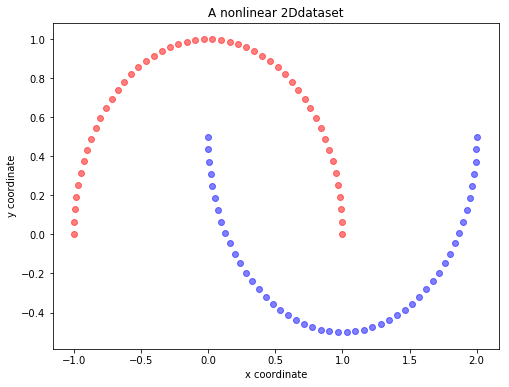
plt.title('A nonlinear 2Ddataset')
plt.ylabel('y coordinate')
plt.xlabel('x coordinate')

plt.show()

위 그림에서 볼 수 있듯, 하프문 데이터는 선형 분류가 불가능한 데이터입니다. 이러한 비선형 데이터에 Linear PCA를 적용하면 다음과 같은 결과가 나타납니다.

from sklearn.decomposition import PCA

scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_spca[y==0, 0], X_spca[y==0, 1], color='red', alpha=0.5)
plt.scatter(X_spca[y==1, 0], X_spca[y==1, 1], color='blue', alpha=0.5)

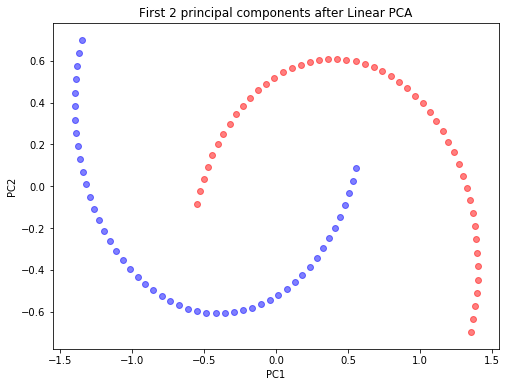
plt.title('First 2 principal components after Linear PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

import numpy as np
scikit_pca = PCA(n_components=1)
X_spca = scikit_pca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_spca[y==0, 0], np.zeros((50,1)), color='red', alpha=0.5)
plt.scatter(X_spca[y==1, 0], np.zeros((50,1)), color='blue', alpha=0.5)

plt.title('First principal component after Linear PCA')
plt.xlabel('PC1')

plt.show()

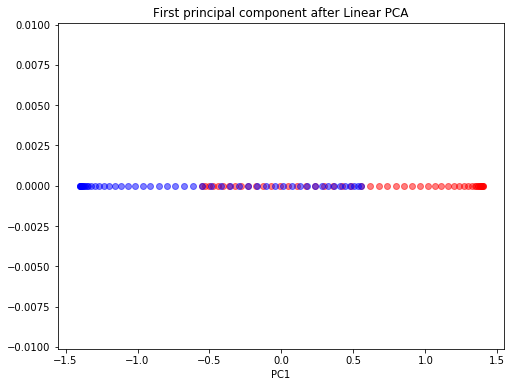
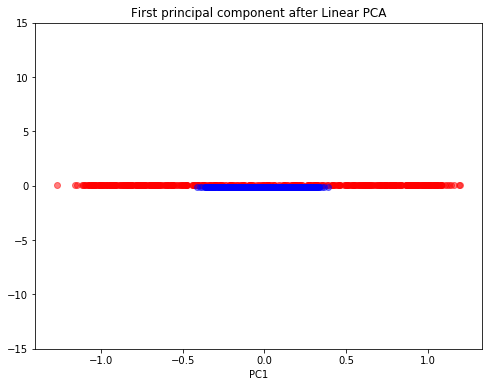
첫번째 그림은 Linear PCA의 결과로 얻어지는 두 개의 주성분 축에 데이터를 projection한 결과를, 두번째 그림은 첫 번째 주성분 축에 데이터를 projection한 결과를 보여줍니다. Linear PCA 결과, 데이터를 선형 분류하는 것은 여전히 불가능합니다. 그렇다면 Kernel PCA를 사용하면 어떤 상반된 결과가 도출될까요? 하프문 데이터에 Gaussian RBF kernel PCA을 사용한 결과는 다음과 같습니다.

from sklearn.decomposition import KernelPCA

scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_skernpca[y==0, 0], X_skernpca[y==0, 1], color='red', alpha=0.5)
plt.scatter(X_skernpca[y==1, 0], X_skernpca[y==1, 1], color='blue', alpha=0.5)

plt.text(-0.48, 0.35, 'gamma = 15', fontsize=12)
plt.title('First 2 principal components after RBF Kernel PCA via scikit-learn')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

scikit_kpca = KernelPCA(n_components=1, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_skernpca[y==0, 0], np.zeros((50,1)), color='red', alpha=0.5)
plt.scatter(X_skernpca[y==1, 0], np.zeros((50,1)), color='blue', alpha=0.5)
plt.text(-0.48, 0.007, 'gamma = 15', fontsize=12)
plt.title('First principal component after RBF Kernel PCA')
plt.xlabel('PC1')
plt.show()

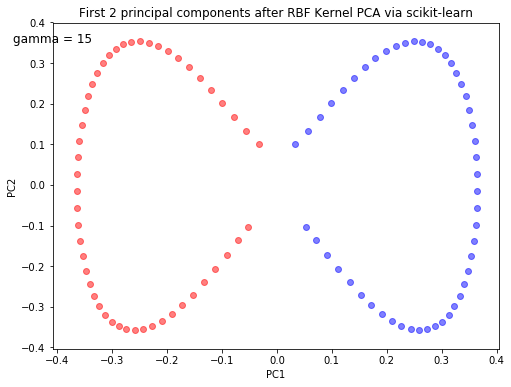
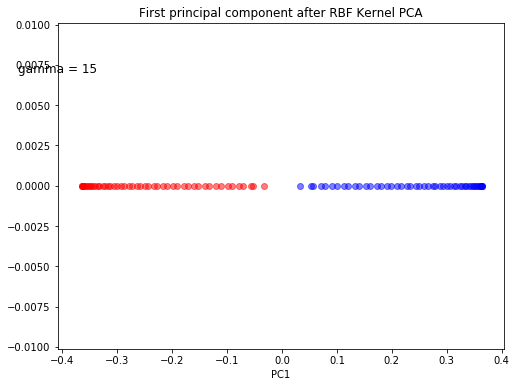
PCA에서와 마찬가지로, 첫번째 그림은 Gaussian RBF kernel PCA의 결과로 얻어지는 두 개의 주성분 축에 데이터를 projection한 결과를, 두번째 그림은 첫 번째 주성분 축에 데이터를 projection한 결과를 보여줍니다. Linear PCA와 달리, 선형 분류가 가능해 졌음을 확인할 수 있습니다.

Concentric circles

from sklearn.datasets import make_circles

X, y = make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)

plt.figure(figsize=(8,6))

#동심원 데이터 생성
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', alpha=0.5)
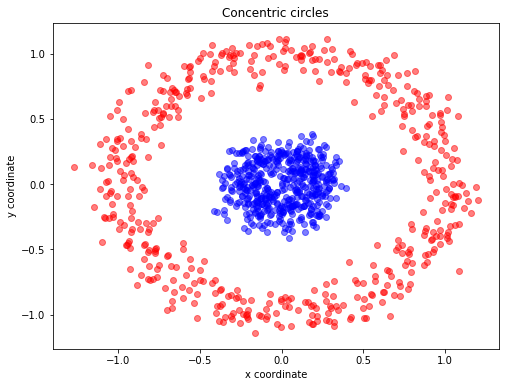
plt.title('Concentric circles')
plt.ylabel('y coordinate')
plt.xlabel('x coordinate')
plt.show()

동심원 데이터 역시 선형 분류가 불가능한 데이터 입니다. 이 데이터에 Linear PCA와 Gaussian RBF kernel PCA를 적용하여 각각의 첫번째 주성분 축에 데이터를 projection한 결과는 다음과 같습니다.

scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X[y==0, 0], np.zeros((500,1))+0.1, color='red', alpha=0.5)
plt.scatter(X[y==1, 0], np.zeros((500,1))-0.1, color='blue', alpha=0.5)
plt.ylim([-15,15])
plt.text(-0.125, 12.5, 'gamma = 15', fontsize=12)
plt.title('First principal component after Linear PCA')
plt.xlabel('PC1')
plt.show()

scikit_kpca = KernelPCA(n_components=1, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_skernpca[y==0, 0], np.zeros((500,1)), color='red', alpha=0.5)
plt.scatter(X_skernpca[y==1, 0], np.zeros((500,1)), color='blue', alpha=0.5)
plt.text(-0.05, 0.007, 'gamma = 15', fontsize=12)
plt.title('First principal component after RBF Kernel PCA')
plt.xlabel('PC1')
plt.show()

Linear PCA와 달리, Gaussian RBF kernel PCA를 시행한 결과 데이터의 선형 분류가 가능해 졌음을 알 수 있습니다.

Swiss roll

from sklearn.datasets.samples_generator import make_swiss_roll
from mpl_toolkits.mplot3d import Axes3D

#스위스 롤 데이터 생성
X, color = make_swiss_roll(n_samples=800, random_state=123)

fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.rainbow)
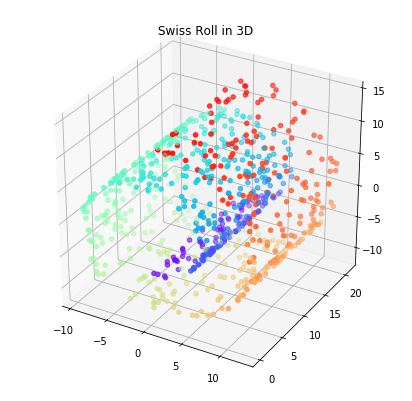
plt.title('Swiss Roll in 3D')
plt.show()

앞서 살펴보았던 하프문, 동심원 데이터는 2차원 상의 데이터였는데요. 이번에는 3차원의 스위스 롤 데이터에 Linear PCA, Gaussian RBF kernel PCA과 polynomial kernel PCA를 적용한 결과를 비교해 보고자 합니다.

scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_spca[:, 0], X_spca[:, 1], c=color, cmap=plt.cm.rainbow)
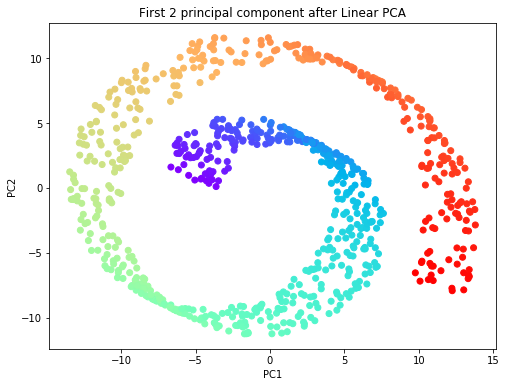
plt.title('First 2 principal component after Linear PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=0.1)
X_skernpca = scikit_kpca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_skernpca[:, 0], X_skernpca[:, 1], c=color, cmap=plt.cm.rainbow)

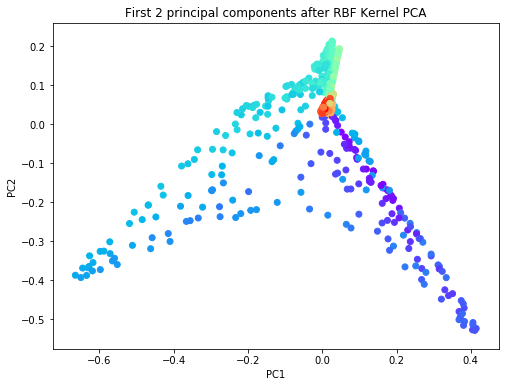
plt.title('First 2 principal components after RBF Kernel PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

scikit_kpca = KernelPCA(n_components=2, kernel='poly', gamma=0.1)
X_skernpca = scikit_kpca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_skernpca[:, 0], X_skernpca[:, 1], c=color, cmap=plt.cm.rainbow)

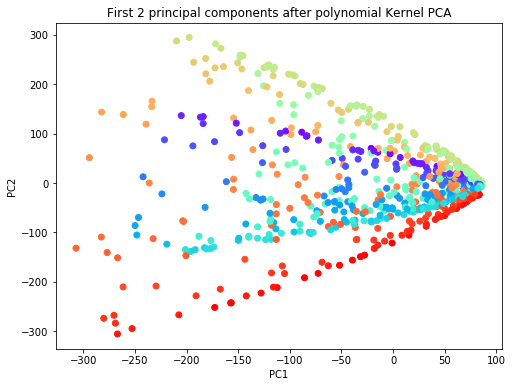
plt.title('First 2 principal components after polynomial Kernel PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

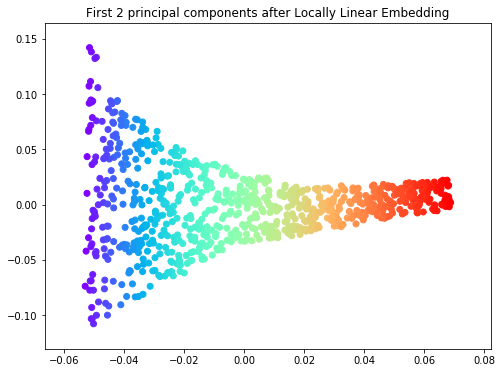
스위스 롤 데이터에 Linear PCA, Gaussian RBF kernel PCA과 polynomial kernel PCA를 적용한 결과, 세 기법 모두 스위스 롤 데이터를 펼친(unroll) 본질적인 특성을 보여주지는 못하고 있습니다. 이러한 한계점을 보완해 줄 있는 비선형 차원축소 기법이 Locally Linear Embedding(LLE)입니다. LLE는 데이터 간의 본질적 거리를 보존하면서 데이터를 고차원에서 저차원 상으로 축소시키는 기법으로, 매니폴드 학습(manifold learning)에 해당합니다. 스위스 롤 데이터에 LLE 기법을 적용한 결과는 다음과 같습니다.

from sklearn.manifold import locally_linear_embedding

X_lle, err = locally_linear_embedding(X, n_neighbors=12, n_components=2)

plt.figure(figsize=(8,6))
plt.scatter(X_lle[:, 0], X_lle[:, 1], c=color, cmap=plt.cm.rainbow)

plt.title('First 2 principal components after Locally Linear Embedding')
plt.show()