Language Model: n-gram에서 RNN으로의 발전
n-gram
Language Model(LM)은 어떤 단어들의 나열 $x^{(1)}, x^{(2)},…, x^{(t)}$ 이 주어졌을 때, 다음 단어 $x^{(t+1)}$가 등장할 확률을 계산하는 모델입니다. 이 때 모든 단어들은 미리 정의한 단어 사전 $V$에 포함되어 있음을 가정합니다.
\[P(x^{(t+1)}|x^{(t)},…,x^{(1)})\]딥러닝 모델 등장 이전에는 n-gram LM을 사용했습니다. 간단히 설명하면, 특정 단어와 그 앞에 등장하는 n-1개 단어들의 조합이 학습용 데이터셋에 얼마나 자주 등장하는지를 세어보는 것입니다. 예를 들어, “오늘은 설날이다. 그래서 떡국을 ___” 라는 단어들의 나열이 주어졌을때 3-gram LM을 학습한다면 아래와 같은 과정을 통해 다음 단어 $w$가 등장할 확률을 계산합니다.
아마도 ‘만들었다’ 혹은 ‘먹었다’가 등장할 확률이 ‘입었다’가 등장할 확률보다는 확실히 높게 나올 것입니다. 이러한 n-gram 모델의 한계점은 첫번째로 정보 손실입니다. 위 예시는 3-gram LM이므로 “오늘은 설날이다.”는 버려집니다. 다음 단어 $w$를 예측하는 데에 오늘이 설날이라는 정보는 매우 유용해보이지만, n-gram LM에서는 이 정보를 잃게 되는 것입니다. 두번째는 학습용 데이터셋에 계산에 필요한 단어들의 나열이 없을 때 계산이 어렵다는 점입니다. count(그래서 떡국을)=0 이면 확률값을 계산할 수 없게 됩니다.
Recurrent Neural Network(RNN)
n-gram 이후 사용된 RNN 모델은 n-gram 모델의 문제점을 개선했습니다. RNN은 고정된 길이의 sequence를 입력할 필요도 없고, count 기반 방식도 아니기 때문입니다.
RNN의 또다른 장점은 $t$시점의 단어를 예측할 때 이전에 등장한 단어들로부터 추출한 hidden state $h_0, h_1,…,h_{t-1}$을 통해 그 정보를 충분히 활용할 수 있다는 점인데요. n-gram처럼 n개 범위 밖에 있는 정보를 잃지 않아도 되는 것입니다. 하지만 실제로 RNN 모델을 학습해 보면, backpropagation 과정에서 gradient가 점점 작아지는 vanishing gradient 문제가 발생합니다. 앞 시점으로 갈수록 weight 업데이트가 거의 일어나지 않는 것입니다. 결과적으로 입력 sequence의 길이가 길어질수록 앞 시점에 나왔던 정보를 잊어버리고 단기 기억만 갖게 됩니다.
LSTM
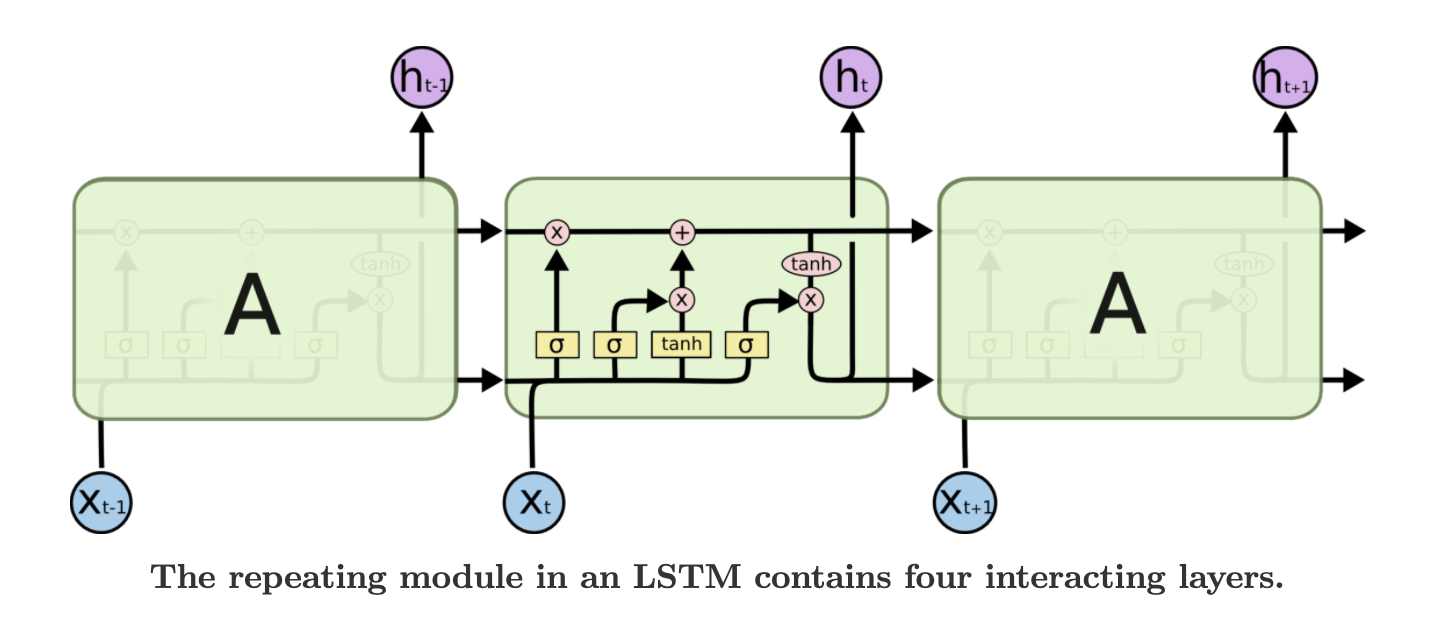
이러한 RNN의 문제점을 해결하기 위한 대표적인 방법이 바로 cell 구조를 LSTM으로 바꾸는 것입니다. LSTM은 RNN의 hidden state $h$ 이외에도 정보를 얼마나 저장할지 결정하는 cell state $c$라는 변수를 사용합니다. 또한 잊어버리거나(forget gate $f$), 기억하거나(input gate $i$), 출력하는(output gate $o$) 정보의 양을 제어하는 gate를 사용하는데요. 각 gate에 sigmod 함수 $\sigma$를 취해서 gate의 output은 0과 1 사이의 값을 갖습니다. 이러한 장치들을 통해 LSTM cell은 RNN 모델이 앞 시점에 나왔던 정보를 보다 오래 기억하도록 도와줍니다.