Meta Learning

Few shot learning

전통적인 supervised learning은 아래와 같은 학습 데이터를 사용해 모델을 학습시킨 다음, 학습 데이터에서 등장한 적 없는 새로운 테스트 데이터로 모델을 평가합니다. 이 때, 테스트 데이터는 학습 데이터에 포함된 class여야 합니다. 예를 들어 아래 학습 데이터로 학습한 분류 모델은 토끼 이미지를 분류해 낼 수 없을 것입니다. 허스키, 코끼리, 호랑이, 앵무새, 차 외에 다른 class의 정보는 모델이 전혀 가지고 있지 않기 때문입니다.

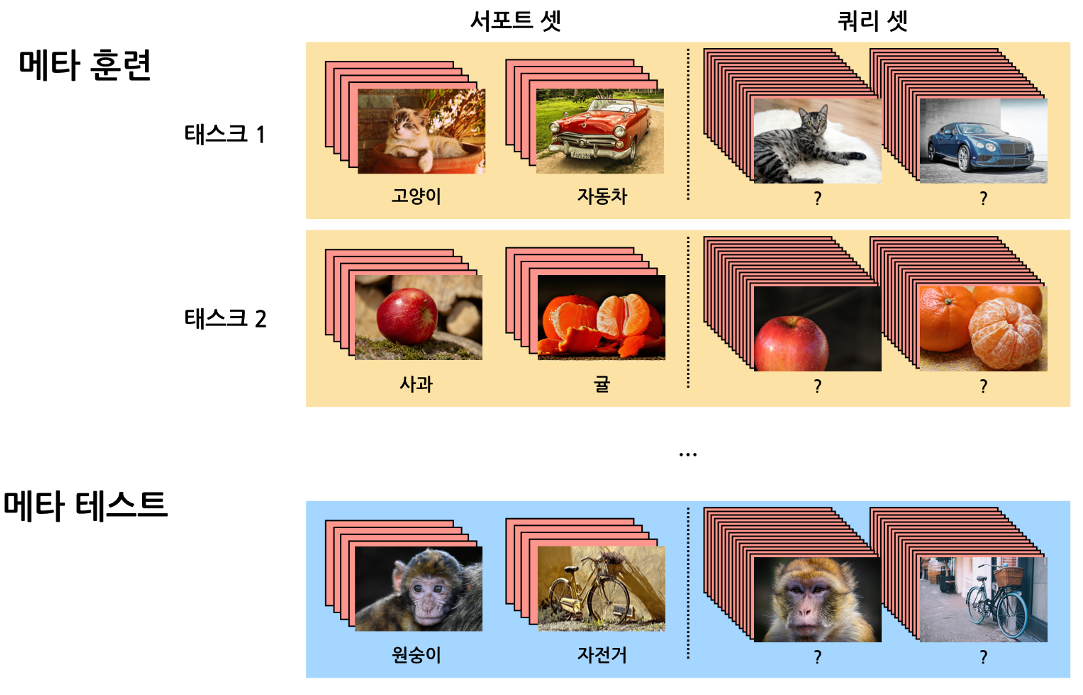
하지만 모델에게 아래와 같은 힌트를 준다면 상황은 달라질 것입니다. 이처럼 대용량 데이터셋으로 학습한 모델에 Support Set이라는 힌트를 주고, 학습 데이터에 포함되어 있지 않은 unknown class의 Query Sample을 제시하는 학습 문제가 few shot learning입니다. 조금 더 구체적으로는, Support Set의 class 개수($N$)와 클래스별 데이터 개수($K$)에 따라 N-way K-shot 문제라고 부릅니다. 아래와 같은 경우는 6-way 1-shot 문제입니다.

Support Set이 주어진다고 해도 모델이 unknown class를 분류하는 것은 쉬운 일이 아닙니다. 딥러닝 모델이 우수한 성능을 달성할 수 있도록 하는 전제 조건은 대용량 데이터셋을 충분히 학습하는 것인데, 이 데이터가 부족하기 때문입니다. 이러한 상황에서 적용할 수 있는 방법 중 하나가 바로 meta learning입니다.

meta learning

meta learning은 적은 양의 데이터만으로도 효율적으로 학습할 수 있도록 모델이 학습 방법을 스스로 학습하는 것입니다. meta learning의 종류는 다음과 같이 나누어 볼 수 있습니다.

• 모델 기반 meta learning: 모델이 작업을 수행하는 방법을 내부적으로 모델링하여, 새로운 task에 더 쉽게 적응하고 빠르게 학습할 수 있도록 만드는 방식
• 최적화 기반 meta learning: 학습 알고리즘 자체를 최적화하여 새로운 task을 더 빠르고 효과적으로 학습할 수 있도록 만드는 방식
• 메트릭 기반 meta learning: 데이터 포인트 간의 유사성이나 차이를 측정하여 데이터 사이의 관계를 이해함으로써 모델이 새로운 task에 더 잘 적응할 수 있도록 만드는 방식

Episodic Learning

episodic learning은 meta learning을 구현하는 방식 중 하나로, 특히 메트릭 기반 meta learning에서 자주 사용됩니다. 이 방식에서는 “episode”라고 불리는 학습의 단위를 사용하여, 각 episode마다 서로 다른 class의 데이터로 구성된 여러 개의 task를 학습합니다. Query Set은 Support Set과 class는 같지만, Support Set에 존재하지 않는 데이터로 구성되어 있는데요. 이러한 방식으로 데이터를 구성하면 실제 테스트 환경을 모방하여 모델 스스로 학습 규칙을 도출할 수 있도록 학습이 진행되기 때문에 일반화 성능을 향상시킬 수 있습니다.

episodic learning 구현 예시

많이들 알고 계신 logistic regression을 사용해 episodic learning을 구현하는 것도 가능합니다.

• step 1 N-way K-shot episode를 샘플링해서 데이터셋을 준비합니다.

• step 2 Support Set으로 모델을 학습합니다. weight matrix $W$와 bias vector $b$는 episode 별로 학습되는 파라미터입니다. regularization 계수 $\lambda$를 모든 episode에서 공유하는 파라미터로 설정해 보겠습니다. 맨 처음에는 $\lambda$를 임의의 값으로 초기화합니다.

\[P(y = c \mid \mathbf{x}) = \frac{\exp\bigl(\mathbf{w}_c^\top \mathbf{x} + b_c)}{\sum_{c}\exp(\mathbf{w}_{c}^\top \mathbf{x} + b_{c})}\] \[L = -\frac{1}{N \cdot K} \sum_{i} \log P(y_i \mid \mathbf{x}_i)+\frac{\lambda}{2}||w||^2\]

• step 3 학습한 모델로 Query set의 class를 예측하고 loss $L$을 계산합니다.

• step 4 $\lambda$에 대해 gradient descent를 수행하여 $\lambda$를 업데이트 합니다. $\eta$는 gradient를 얼마나 크게 반영할지 결정하는 learning rate입니다.

\[\lambda \leftarrow \lambda - \eta \cdot \frac{\partial L_{\text{query}}(\lambda)}{\partial \lambda}\]

• step 5 위 과정을 여러 episode에 걸쳐 반복하면서 $\lambda$를 최적화합니다. 여러 episode의 경험을 공통 파라미터 $\lambda$에 축적하여 few-shot 상황에서 빠르고 robust하게 학습을 가능하게 만드는 것입니다.

위와 같이 neural network 없이도 meta learning을 구현할 수는 있지만, neural network를 활용하면 그 효과를 증폭시킬 수 있습니다. 다음 포스트에서는 neural network를 활용한 메트릭 기반 meta learning에 대해 알아보겠습니다.

Reference

• Stanford CS330: Deep Multi-Task & Meta Learning
• Few-Shot Learning