[Paper Review] On Pixel-Wise Explanations for Non-Linear Classifier Desisions by Layer-Wise Relevance Propagation

• 비선형성 때문에 분류 결과가 어떻게 도출되었는지 자세한 정보를 제공하지 못함 → 예측 결과(value)를 분해해서 이미지 픽셀 각각의 기여도를 구한 다음, heatmap으로 시각화
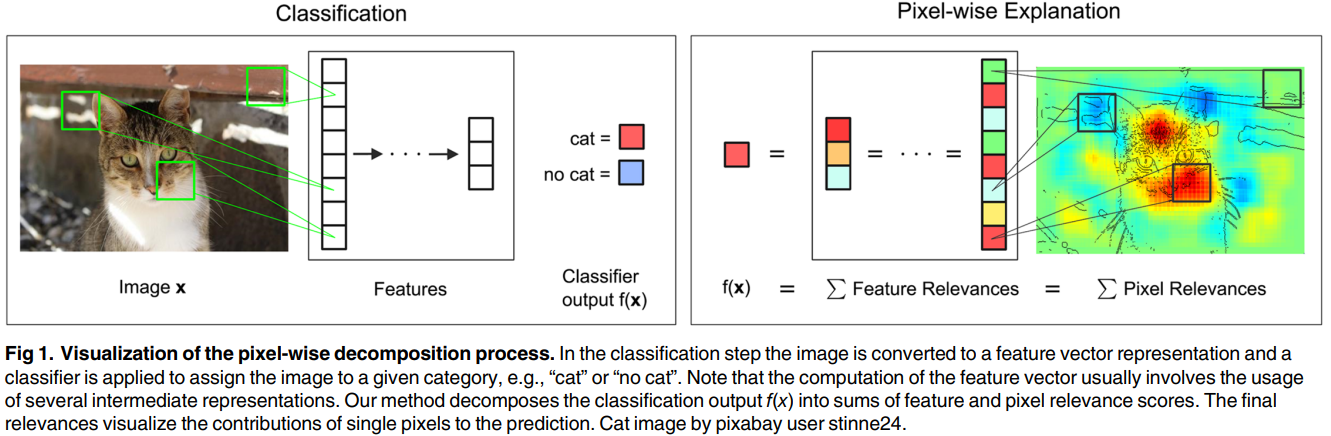
• pre-trained model에 적용하는 방식
• pixel-wise training이나 pixel-wise labeling 불필요
• layer-wise relevance propagation can be done without the need to use an approximation by means of Taylor expansion.

다른 방법론들과의 비교

기존 연구인 sensitivity 와의 차별점

• sensitivity는 LRP와 달리 slope decomposition (gradient-based)
• sensitivity의 relevance score $R$은 이미지 픽셀 각각의 변화가 분류 결과를 얼마나 증가 혹은 감소시키는지 (얼마나 sensitive한지) 나타냄
• 분류 결과(value) 자체를 설명하는 것이 아니라 분류 function의 variation을 설명
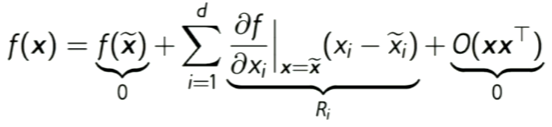
• 위 이미지에서 LRP는 relevance가 차에 집중되어 있는 반면, sensitivity는 relevance가 이미지 전반에 산재되어 있음

Deep Taylor Decomposition과의 차이

• Taylor decomposition 방법을 통해 분류 결과(value)를 분해하는 방법
• Simple taylor는 다음과 같은 이유로 deep neural network에서 잘 작동하지 않음
  • $f(\tilde x)=0$을 만족하는 root point $\tilde x$를 찾기 어려움
  • network가 깊어질수록 gradient에 noise가 섞이는 문제(gradient shattering problem)
• 그래서 나온 것이 Deep taylor decomposition
  • LRP처럼 최종 분류 결과 $f(x)$를 decomposition해서 한 번에 relevance score $R$을 얻는 것이 아님
  • neural network는 단순한 function들의 조합으로 이루어져 있기 때문에, 각각의 layer를 sub function으로 분해해서 분류 결과 $f(x)$를 각 뉴런의 taylor decomposition으로 나눈 다음, 그 결과를 합쳐서 approximation하는 방법

Pixel-wise Decomposition

• 각 뉴런은 어느 정도의 기여도 $R$을 가지고 있음
• 기여도는 top-down 방식으로 각 뉴런의 출력단에서 입력단 방향으로 재분배됨
• 보존 특성(conservation property)이라는 아이디어를 사용해서 hidden layer 각각의 relevance 총합이 일치하게 함

\[f(x)=R_7^{(3)}=R_3^{(2)}+R_4^{(2)}+R_5^{(2)}\] \[=R_1^{(1)}+R_2^{(1)}+R_3^{(1)}\]

Layer-wise relevance propagation(LRP)

• $f(x)$는 입력 이미지 $x$에 대한 예측 결과이고, $R_d$는 hidden layer를 구성하는 원소 $d$의 relevance일 때, $f(x)$는 모든 원소들의 relevance의 합으로 분해할 수 있다. ($V$는 dimension)

\[f(x) \approx \sum_{d=1}^{V}R_d\]

• $R_d$가 양수이면 feature $d$는 예측 결과에 긍정적 영향을 주는 요소이고, 반대로 $R_d$가 음수이면 feature $d$는 예측 결과에 부정적 영향을 주는 요소라고 해석할 수 있다. 아래 이미지는 neural network 분류 모델의 마지막 layer에서 class 3에 해당하는 노드의 값을 분해한 결과(왼쪽)과 class 9에 해당하는 노드의 값을 분해한 결과(오른쪽)이다. 오른쪽 그림에서 파란 부분은 $R_d$가 음수인 부분으로, 해당 이미지를 왜 class 9으로 분류할 수 없는지 보여준다.

• 최종적으로 우리가 구하고자 하는 것은 입력 이미지(첫번째 layer) 픽셀 각각의 relevance이므로 $R_d^{(1)}$으로 표현할 수 있다. 그리고 모든 픽셀 $x_{(d)}$에 대한 $R_d^{(1)}$의 합이 곧 $f(x)$이다. 하지만 $f(x)$와 $R_d^{(1)}$사이에는 여러 개의 hidden layer가 존재하므로 $f(x)$에서 $R_d^{(1)}$를 바로 구할 수 없다.

\[f(x) = \dots = \sum_{d\in{l+1}}R_d^{(l+1)} = \sum_{d\in{l}}R_d^{(l)} = \dots = \sum_dR_d^{(1)}\]

\[R_i^{(l)}=\sum R_{i \gets k}^{(l, l+1)}\]

• 위 수식에서 $R_{i \gets k}^{(l, l+1)}$는 $l$번째 layer와 $l+1$번째 layer를 연결하고, $l+1$번째 layer의 $k$ 노드로부터 $l$번째 layer의 $i$ 노드로 전파되는 relevance를 의미한다. 예를 들어, $R_3^{(1)}=R_{3 \gets 6}^{(1,2)} + R_{3 \gets 5}^{(1,2)}$이다. 노드 간 전파되는 relevance인 $R_{i \gets k}^{(l, l+1)}$를 구하면 특정 layer, 특정 node의 relevance를 계산할 수 있는 것이다. $R_{i \gets k}^{(l, l+1)}$는 다음과 같이 구할 수 있다.

\[a_7=f(x)=w_{47} \times a_x + w_{57} \times a_5 + w_{67} \times a_6\] \[f(x)=a_7=R_7^{(3)}=R_7^{(3)} \times \frac {f(x)}{f(x)}\] \[=R_7^{(3)} \times\frac {w_{47}a_4 + w_{57}a_5 + w_{67}a_6}{w_{47}a_4 + w_{57}a_5 + w_{67}a_6}\] \[= R_7^{(3)} \times \frac {w_{47}a_4}{w_{47}a_4 + w_{57}a_5 + w_{67}a_6}\] \[+ R_7^{(3)} \times \frac {w_{57}a_5}{w_{47}a_4 + w_{57}a_5 + w_{67}a_6}\] \[+ R_7^{(3)} \times \frac {w_{67}a_6}{w_{47}a_4 + w_{57}a_5 + w_{67}a_6}\]

• 다시 말해서 분류 결과인 $f(x)$를 $\sum_ia_iw_{i7}$으로 정규화한 것으로, 다음과 같이 정리할 수 있다.

\[R_4^{(2)}=R_{4 \gets 7}^{(2,3)}=R_7^{(3)} \times \frac {w_{47}a_4}{w_{47}a_4 + w_{57}a_5 + w_{67}a_6}\] \[R_5^{(2)}=R_{5 \gets 7}^{(2,3)}=R_7^{(3)} \times \frac {w_{57}a_5}{w_{47}a_4 + w_{57}a_5 + w_{67}a_6}\] \[R_6^{(2)}=R_{6 \gets 7}^{(2,3)}= R_7^{(3)} \times \frac {w_{67}a_6}{w_{47}a_4 + w_{57}a_5 + w_{67}a_6}\]

• 위 수식을 일반화하면 다음과 같다.

\[R_{i \gets k}^{(l,l+1)} = R_k^{(l+1)} \frac {a_iw_{ik}}{\sum_ha_hw_{hk}}\]

Pixel-wise Decomposition for Classifiers over Bag of Words Features

Vision 분야에 Bag of Words 적용

• Bag of Words 모델은 단어들의 순서에 관계없이, 단어들의 빈도수로 문서를 표현하는 방법
  • 문서들은 다수의 동일한 키워드들을 공유하고, 그 키워드들은 순서에 관계없이 서로 연관되어 있음
• 이 컨셉을 Vision 분야에 적용하면, 순서가 없는 이미지 패치들의 묶음으로 이미지를 표현하는 것

Bag of Words models 진행 과정

• Step 1 local feature 추출

• Step 2 local feature들의 representatives 계산
  

  • 문서의 vocabulary와 같은 기능 (visual words)
  • 예를 들어, k-means clustering으로 cluster centroids를 계산할 수 있고, 이 경우 cluster의 개수 = vocabulary size
• Step 3 BoW representation $x$를 얻기 위해 local feature들의 통계량 계산
  
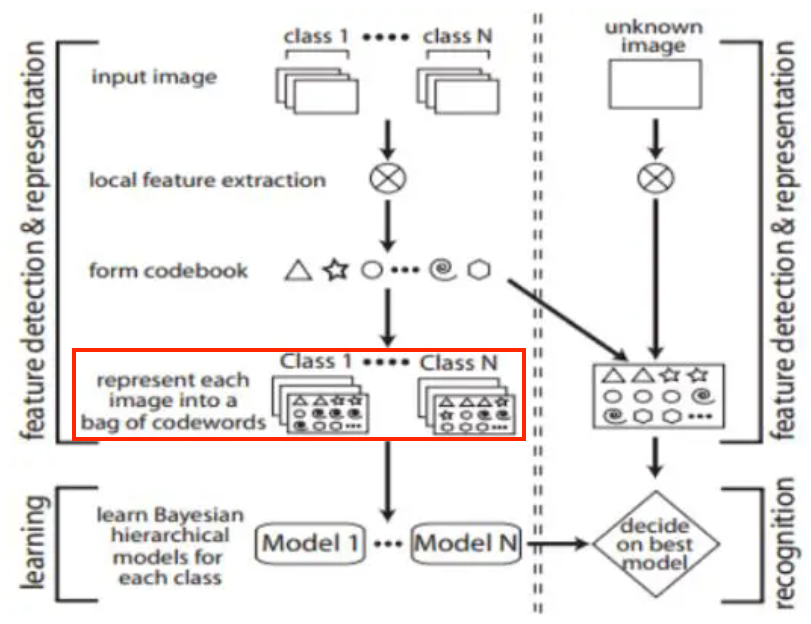
  • step 2에서 구한 visual words들로 각각의 이미지를 표현
  • 위 과정을 수식으로 표현하면 다음과 같음 \(x_{(d)}=(M^{-1}\sum_{j=1}^M{({m_{(d)}(l_j)})}^p)^{\frac{1}{p}}\)
  • mapping function $m$을 통해 local feature $l$을 BoW 공간에 projection해서 BoW representation $x$를 계산
  • $p=1$이면 sum-pooling, $p=\infty$이면 max-pooling

• Step 4 BoW representation $x$에 classifier를 적용

  • 본 논문에서 제안하는 방식은 kernel 방식 기반의 classifier에 적용할 수 있고, 다중 kernel을 사용하는 경우에도 적용 가능
  • 본 논문에서 사용한 classifier는 SVM

Decomposition 과정

• 요약하면 kernel 기반 classifier의 예측값 $f(x)$를 local feature의 기여도($R_l^{(2)}$), 나아가서는 이미지 픽셀 각각의 기여도($R_q^{(1)}$)로 분해하는 과정
• 구체적인 진행 과정
  • Step 1 모든 BoW feature들에 대한 relevance 구하기
    • Relevance scores for sum decomposable kernels
    • Relevance scores for differentiable kernels
  • Step 2 모든 local feature들에 대한 relevance 구하기
    • Local feature scores for sum pooling ($p=1$)
    • Local feature scores for p-means pooling
  • Step 3 모든 이미지 픽셀들에 대한 relevance 구하기

Pixel-wise Decomposition for Multilayer Networks

• 1에서 설명했듯 보존 특성(conservation property)에 의해 모든 layer의 relevance 총합은 동일
• activation function 적용 전 값 $z$를 이용해 relevance $R$ 계산

\[z_{ij}=x_iw_{ij}\] \[z_j=\sum_iz_{ij}+b_j\] \[R^{(l,l+1)}*{i \gets j}=\frac {z*{ij}}{z_j} \cdot R_j^{(l+1)}\] \[R_i^{(l)}=\sum_jR_{i \gets j}^{(l,l+1)}\]

Reference

• Towards Interpretable Deep Learning - Dr. Wojciech Samek - YouTube