PCA

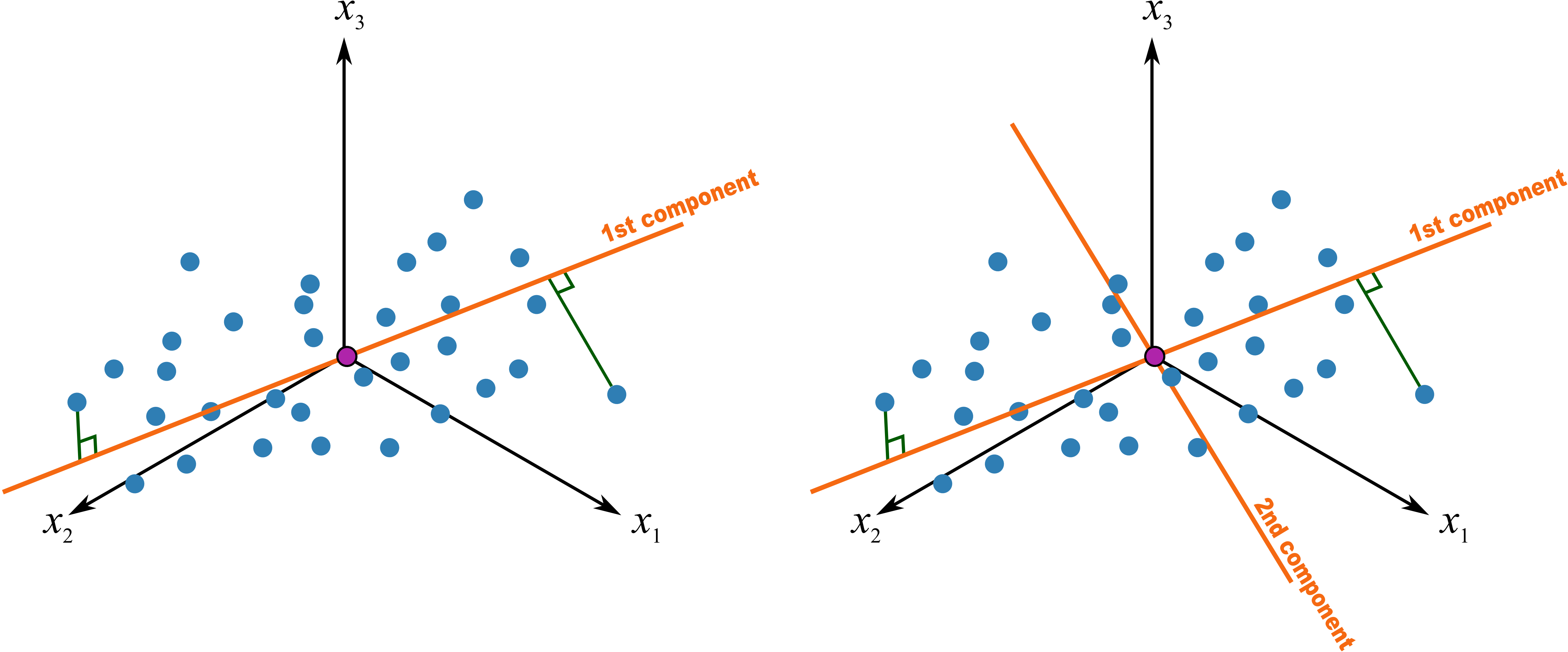
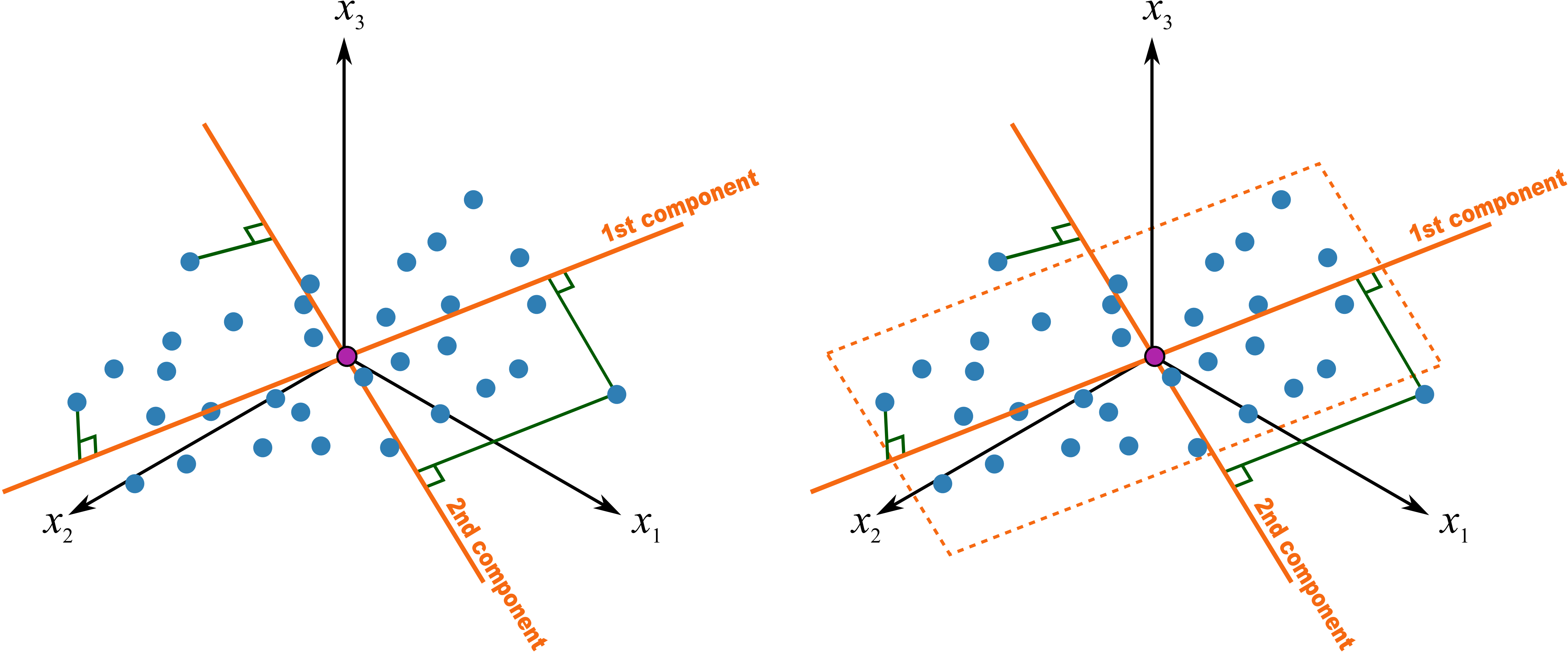
이번 포스트에서는 대표적인 차원 축소 기법 중 하나인 PCA에 대해 살펴보겠습니다. PCA는 주어진 데이터의 분산을 최대한 보존하면서 고차원 상의 데이터를 저차원 데이터로 변환하는 기법입니다. 아래 그림(출처)에서와 같이 데이터의 분산을 최대한 보존하는, 서로 직교(orthogonal)하는 축(component)을 찾고 그 축에 데이터를 projection함으로써 데이터의 차원을 줄이는 동시에 데이터에 포함되어 있는 noise를 제거할 수 있습니다. 아래 예시에서는 3차원이었던 데이터를 2개의 축(1st component와 2nd component)에 projection함으로써 2차원 데이터로 변환하는 과정을 보여주고 있습니다.

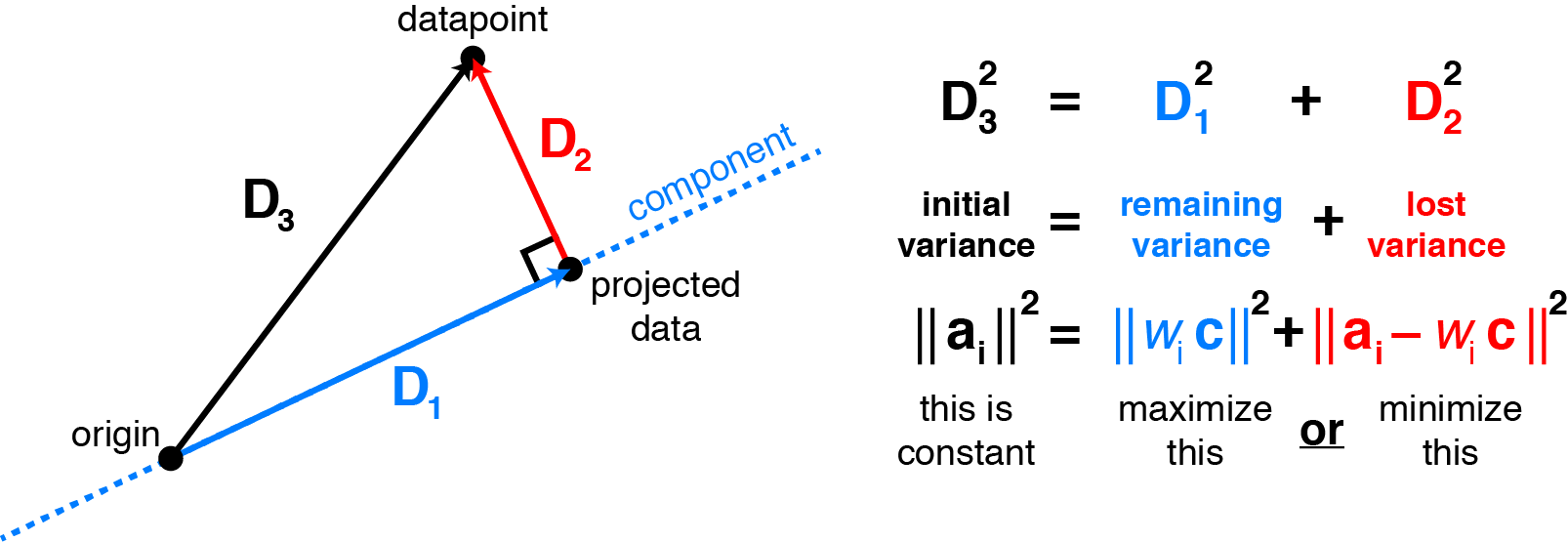
PCA에서 데이터를 projection하는 축(compoenet)에 대하여 좀 더 자세히 살펴보겠습니다. 이 축은 ‘데이터의 분산을 최대한 보존하는 특성을 갖는다’라고 앞서 언급한 바 있는데요. 이는 곧 ‘data point와 projected data의 거리(residual)를 최소화하는 특성을 갖는다’는 말과 같다고 볼 수 있습니다. 원데이터의 분산($D_3$), 축에 의해 보존되는 분산($D_1$)과 projection 과정에서 손실되는 분산($D_2$)은 다음(출처)과 같은 관계에 있기 때문입니다.

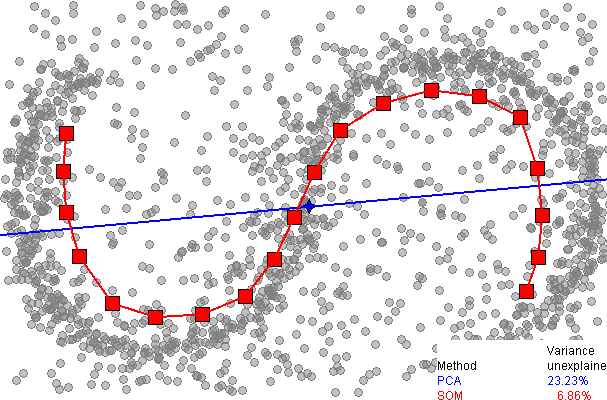
다시 말해 PCA의 목적은 데이터의 분산을 최대한 보존하는, data point와 preojected data의 거리를 최소화하는 linear subspace를 찾는 것입니다. 그런데 PCA를 비선형 데이터에 적용하면 어떻게 될까요? 아래 그림(출처)은 PCA와 비선형 차원 축소 기법인 Self Organizing Map(SOM)에 비선형 데이터를 적용한 결과를 비교하여 보여주고 있습니다.

그림에서 볼 수 있듯이, SOM을 이용하면 많은 양의 분산을 설명할 수 있습니다. 반면에, PCA를 이용하여 데이터를 파란 축에 projection하면 많은 양의 분산($D_2$)이 손실될 것입니다. 따라서 PCA는 비선형 데이터에 적합하지 않은 한계점을 갖습니다. 다음 포스트에서는 PCA의 한계점에 대한 대안으로 사용할 수 있는, Kenel PCA 기법에 대해 알아보겠습니다.