Post

[Paper Review] ReConPatch : Contrastive Patch Representation Learning for Industrial Anomaly Detection

Posted Updated
By jieun choi
19 min read
[Paper Review] ReConPatch : Contrastive Patch Representation Learning for Industrial Anomaly Detection

1. Introduction

이상 탐지는 사전에 수집한 데이터를 바탕으로, 정상 케이스와 비정상 케이스를 구분하는 방법을 학습하는 모델인데요. 비정상 케이스가 희박하고, 학습 데이터와는 다른 새로운 유형의 비정상 케이스가 발견되는 등 데이터셋에 문제가 있는 경우가 많기 때문에 분석에 어려움이 있습니다. 이러한 배경으로 이상 탐지 방법론은 정상 데이터만을 학습에 사용하는 one-class classification 방향으로 발전해 왔습니다. one-class classification의 주요 컨셉은 데이터 간의 거리 metric을 학습시켜서 정상 데이터와의 거리가 먼 데이터를 비정상 데이터로 검출하는 것입니다. 데이터 간의 거리 metric을 학습하는 방법은 크게 두 가지로 나눌 수 있습니다.

  • reconstruction-based approach
    • 원본 데이터와 reconstructed 데이터 사이의 reconstruction error를 측정하는 방법입니다.
    • Autoencoder와 GAN 등이 여기에 속합니다.
  • 대규모 이미지 데이터셋을 pre-train한 모델에서 representation을 추출
    • 데이터가 부족한 상황에서 사용할 수 있는 방법입니다. pre-trained 모델은 이미 다양한 시각적 특성을 학습했기 때문에, 새로운 산업 데이터셋에 빠르게 적응하고, 관련 있는 feature를 추출하는 데 도움을 줄 수 있습니다.
    • 여기에서 관련 있는 feature을 추출한다는 것은 pre-trained 모델에서 산업용 이상 탐지에 필요한 feature만을 선택적으로 추출하여 사용한다는 의미입니다.

pre-trained 모델이 다양한 객체, 풍경, 동물 등을 포함하여 광범위한 시각적 feature를 학습하지만, 이 feature는 어디까지나 학습에 사용된 데이터셋에 최적화된 feature라는 한계가 있습니다. 즉, 이 feature들의 분포는 이상 탐지 모델을 실제로 적용하고자 하는 분석 대상 데이터의 feature 분포와는 차이가 있을 수 있습니다. 이상 탐지 모델의 성능을 향상시키기 위해서는 정상과 비정상의 경계에 놓여있는 결함을 효과적으로 판별할 수 있는 representation space를 학습하는 것이 필수적입니다. 그런데 pre-trained 모델이 학습한 feature는 분석 대상 이미지의 미묘한 결함을 판별하기엔 충분하지 않습니다.

pre-trained 모델의 학습에 사용된 데이터셋과 분석 대상 데이터셋의 분포 차이를 줄이기 위해서는, pre-trained 모델의 representation을 재생산하는 student 모델을 학습시켜 이 모델에서 feature를 추출하는 방법을 사용할 수 있는데요. 하지만 random crop, random rotation, color jitter같은 input augmentation가 여전히 필요하다는 한계점이 있습니다.

본 논문에서 제안하는 ReConPatch는 pre-trained 모델에서 추출한 feature들의 linear modulation을 학습함으로써 이러한 문제점을 해결하고자 합니다. 또한 분석 대상 데이터에 최적화된 동시에 정상과 비정상을 확실히 구분할 수 있는 feature를 수집하기 위해서 contrastive learning 방식을 사용했습니다. 마지막으로, patch feature들 사이의 similarity를 평가하는 지표로써 pairwise similarity와 contextual similarity를 함께 사용했다는 점이 특징입니다.

2. Method

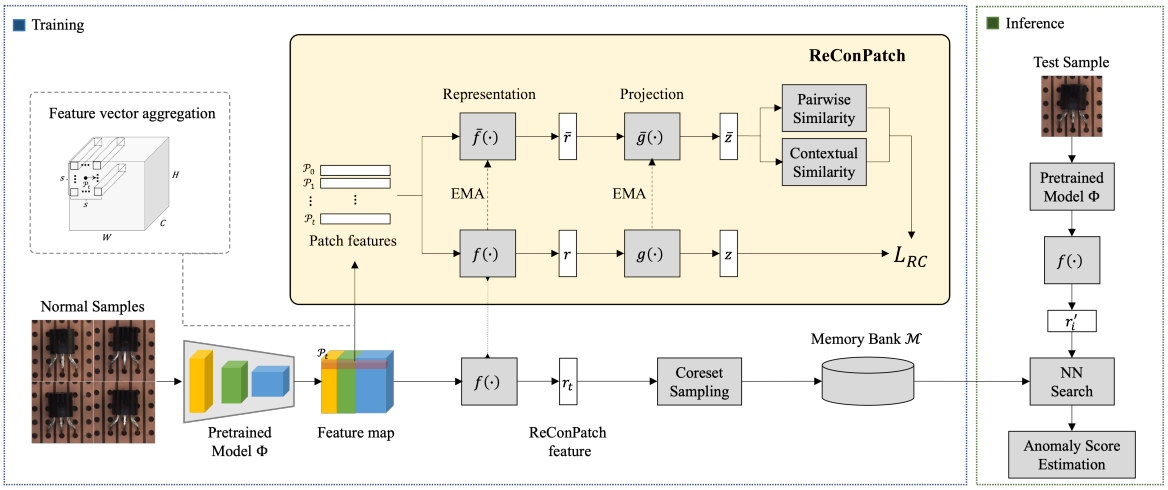
2.1 Overall structure

training phase

  • PatchCore와 같은 방식으로 Patch-level feature $\mathcal{P}(x, h, w) \in \mathbb{R}^{C^\prime}$를 만듭니다.
  • pre-trained CNN 모델의 여러 layer에서 input $x$의 feature map을 추출합니다. layer 별로 feature map의 크기가 다르기 때문에, 크기를 맞춰주고 이어 붙입니다. 이러한 방식으로 생성한 locally aware feature는 patch size $s$ 안에서 이웃한 feature vector들을 aggregate하는 효과가 있습니다.
  • 학습 과정에서 사용하는 network는 두 가지 입니다.
    • relaxed contrastive loss $L_{RC}$를 통해 patch-level feature를 학습합니다. feature representation layer $f$와 projection layer $g$로 이루어져 있습니다.
    • patch-level feature 사이의 pairwise similarity와 contextual similarity를 계산합니다. feature representation layer $\bar{f}$와 projection layer $\bar{g}$로 이루어져 있습니다.
  • 위와 같은 과정을 통해 학습한 feature representation layer $f$에 pre-trained CNN에서 추출한 patch-level feature를 통과시키면 target-oriented feature를 얻을 수 있습니다. 다시 말해 분석 대상 데이터셋에 최적화된 patch-level feature를 구할 수 있는 것입니다.
  • 학습이 완료되면 feature representation $f$에서 greedy approximation algorithm 기반의 subsampling 방식으로 coreset이 샘플링되고, Memory Bank $\mathcal{M}$에 저장됩니다.

inference phase

  • training phase와 동일하게 테스트 데이터의 feature를 구한 다음, 이 feature를 memory bank의 정상 이미지들의 feature와 비교해서 anomaly score를 산출합니다.

2.2 Patch-level feature representation learning

similarity metric

본 논문에서는 feature representation을 학습하기 위해 contrastive learning 방식을 사용했습니다. 그런데 contrastive learning을 사용하면 정상 데이터들의 variation을 모델링하게 되므로, false-positive rate이 증가할 수 있다는 단점이 있습니다. contrastive learning 방식을 사용하여 유사한 데이터 포인트는 similarity가 높게, 상이한 데이터 포인트는 similarity가 낮게 학습하기 위해서는 어떤 데이터들이 서로 유사하고, 어떤 데이터들이 서로 상이한지를 라벨링한 데이터셋(labeled pair)이 필요한데요. 현실적으로 이러한 데이터를 구하는 것은 쉽지 않습니다. 저자들은 이러한 문제를 해결하기 위해서 feature들 사이의 pairwise similarity와 contextual similarity를 학습 과정에서 pseudo-label로 사용했습니다.

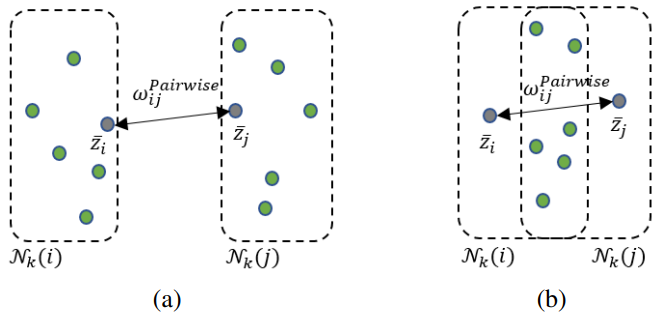
case (a)에서 $\mathcal{N}_k(i)$와 $\mathcal{N}_k(j)$는 서로 겹치지 않지만 case (b)에서는 $\mathcal{N}_k(i)$와 $\mathcal{N}_k(j)$는 서로 겹칩니다. 이러한 차이로 두 case에서 $\bar{z_i}$와 $\bar{z_j}$의 pairwise similarity는 동일하지만 contextual similarity는 다릅니다. case (a)에서 $\bar{z_i}$와 $\bar{z_j}$는 서로 다른 그룹에 포함되므로 similarity가 낮아야(거리가 멀어야) 하고, case (b)에서 $\bar{z_i}$와 $\bar{z_j}$는 같은 그룹에 포함되므로 similarity가 높아야(거리가 가까워야)하는데, pairwise similarity로는 이러한 관계성을 파악할 수 없습니다. pairwise similarity의 한계점을 보완하는 metric으로써 contextual similarity를 사용했습니다.

  • final similarity
    • pairwise similarity로 feature 그룹 간 관계를 파악하기에는 부족함
    • 두 데이터 포인트가 nearest neighbor를 많이 공유할수록 contextual similarity가 높아짐

    • pairwise similarity와 contextual similarity의 linear combination

      \[w_{ij}=\alpha \cdot w_{ij}^{Pairwise}+(1-\alpha) \cdot w_{ji}^{Contextual}, \alpha \in [0, 1]\]

    • pairwise similarity

      \[w_{ij}^{Pairwise}=e^{-||\bar{z_i}-\bar{z_j}||^2_2/\sigma}\]

    • contextual similarity

      \[\tilde{w_{ij}}^{Contextual}=\begin{cases}\frac{\mathcal{N}_k(i) \cap \mathcal{N}_k(j)}{\mathcal{N}_k(i)}, & j \in \mathcal{N}_k(i) \\ 0, & otherwise \end{cases}\]

relaxed contrastive loss

patch-level feature는 이웃한 patch들과의 상관관계를 내포하고 있기 때문에 OK, NG와 같이 명시적인 라벨을 가지지 않습니다. 더욱이 ReConPatch의 목표는 feature들을 명확히 구분하는 것이라기 보다는 분석 대상 데이터셋에 최적화된 feature를 구하는 것입니다. 따라서 저자들은 relaxed contrastive loss를 사용했습니다. relaxed contrastive loss에서는 inter-feature similarity $w$가 psedo-label로 사용됩니다.

두 patch vector $z_i$와 $z_j$의 거리

\[\delta_{ij}=\frac{||z_i-z_j||_2}{\frac{1}{N}\sum^N_{n=1}||z_i-z_n||_2}\]

위 수식에서 $z_i$는 $i$번째 patch의 embedding vector를 의미하고, $z_j$는 $j$번째 patch의 embedding vector를 의미합니다. $\delta_{ij}$는 두 vector의 유클리디안 거리를 $z_i$와 나머지 모든 vector들과의 유클리디안 거리 평균으로 나눈 값으로, $z_i$와 $z_j$의 상대적 거리를 나타냅니다.

  • $\delta_{ij}$가 0에 가까운 경우: $z_i$와 $z_j$의 거리가 평균 거리보다 작음
  • $\delta_{ij}$가 1에 가까운 경우: $z_i$와 $z_j$의 거리가 평균 거리와 유사함
  • $\delta_{ij}$가 1보다 큰 경우: $z_i$와 $z_j$의 거리가 평균 거리보다 큼

relaxed contrastive loss

\[\mathcal{L}_{RC}(z)=\frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}w_{ij}\delta_{ij}^2+(1-w_{ij})max(m-\delta_{ij},0)^2\]
  • $N$: 총 데이터 수
  • $w_{ij}$: 두 vector $z_i$와 $z_j$의 inter-feature similarity
    • $w_{ij}$가 크면 (=두 vector가 서로 유사하면) $\delta_{ij}^2$항의 영향력이 상대적으로 커짐
      • 두 vector $z_i$와 $z_j$ 사이의 상대적 거리 $\delta_{ij}$가 멀 때 loss 증가
      • 두 vector $z_i$와 $z_j$ 사이의 거리를 최소화하는 방향으로 학습
    • $w_{ij}$가 작으면 (=두 vector가 서로 상이하면) $(1-w_{ij})max(m-\delta_{ij},0)^2$ 항의 영향력이 상대적으로 커짐
      • 두 vector $z_i$와 $z_j$ 사이의 상대적 거리 $\delta_{ij}$가 $m$보다 가까울 때 loss 증가
      • 두 vector $z_i$와 $z_j$ 사이의 거리를 늘려서 보다 명확하게 구분하는 방향으로 학습
  • $\delta_{ij}$: 두 vector $z_i$와 $z_j$의 정규화된 거리
  • $m$: 마진 값. $\delta_{ij}$가 이 값 이하일 때만 유사한 쌍으로 간주됨

2.3 Anomaly detection with ReConPatch

PatchCore와 같은 방식으로 anomaly score를 산출합니다.

  • pixel-wise anomaly score
  • memory bank $\mathcal{M}$의 nearest coreset $r^*$와 representation layer의 output $f(p_t)$의 거리
  • image-wise anomaly score
  • 이미지 내의 모든 patch feature들의 anomaly score의 최댓값

anomaly detection의 정확도는 score-level 앙상블로 향상시킬 수 있습니다. 각각의 모델은 서로 다른 score 분포를 가지고 있기 때문에 정규화(modified z-score)를 수행합니다. 정규화된 anomaly score $\bar{s_t}$는 다음과 같이 정의할 수 있습니다.

\[\bar{s_t}=\frac{s_t-\tilde{s}}{\beta \cdot MAD}\]

위 수식에서 $\tilde{s}$는 anomaly score의 median이고, MAD는 전체 학습 데이터셋에 대한 Mean Absolute Deviation입니다. $\beta$는 constant scale factor로, 저자들이 설정한 값은 1.4826입니다.

3. Experiments and analysis

3.1 Experimental setup

Dataset

MVTec AD

  • 클래스 15개
  • 학습 데이터 3629개
  • 테스트 데이터 1725개

BTAD

  • 클래스 3개
  • 학습 데이터 2540개
  • 테스트 데이터 691개

Metrics

  • Anomaly detection 성능 지표: image-lebel AUROC
  • 테스트 이미지의 anomaly score와 클래스(정상/비정상) 예측 결과 사용
  • Segmentation 성능 지표: pixel-level AUROC
  • 테스트 이미지 내 모든 픽셀의 anomaly score 사용

Implementation details

  • single model
    • feature extractor 파라미터
      • patch size $s$: 3
      • ImageNet pre-trained model
        • WideResNet-50
      • hierarchy level: 2, 3
      • output size: 512
    • coreset subsampling percentage: 1%
    • 학습 파라미터
      • 각각의 클래스에 대해 120 epoch씩 학습
      • optimizer: AdamP with a cosine annealing scheduler
      • learning rate: 1e-5 with a weight decay of 1e-2
  • ensemble model
    • feature extractor 파라미터
      • patch size $s$: 3
      • ImageNet pre-trained model
        • WideResNet-101
        • ResNext-101
        • DenseNet-201
      • hierarchy level: 2, 3
      • output size: 384
    • coreset subsampling percentage: 1%
    • 학습 파라미터
      • 각각의 클래스에 대해 60 epoch씩 학습
      • optimizer: AdamP with a cosine annealing scheduler
      • learning rate: 1e-6 with a weight decay of 1e-2

3.2 Ablation study

coreset subsampling percentage

  • coreset subsampling percentage가 1%일 때 가장 좋은 성능을 보였습니다.

f layer의 output dimension

  • PatchCore는 output dimension이 1024일 때, ReConPatch는 512일 때 가장 좋은 성능을 보였습니다.
  • 모든 dimension 설정에서 ReConPatch의 성능이 PatchCore보다 높았습니다.
  • ReConPatch는 dimension이 64일때 조차도 성능이 크게 떨어지지 않았습니다.

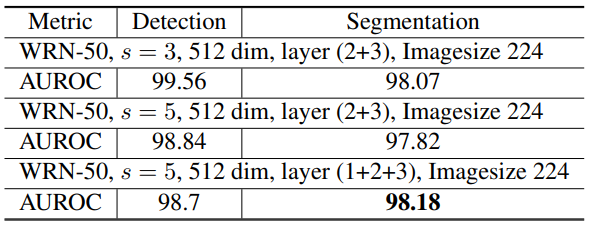
hierarchy level과 patch size

  • patch size를 5로, hierarchy level을 1, 2, 3으로 설정했을 때 Detection 성능이 거의 떨어지지 않으면서 Segmentation 성능이 가장 높았습니다.

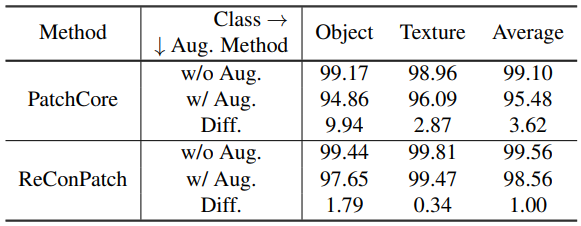
이미지 품질에 따른 모델 성능 차이 실험

  • 현실 상황에서는 다양한 환경적 요인이 이미지의 품질에 영향을 줄 수 있습니다. 이러한 상황을 실험해보기 위해 데이터에 랜덤하게 data augmentation을 적용해 시뮬레이션을 진행했습니다.
  • ReConPatch가 PatchCore에 비해 data augmentation 여부에 따른 성능 차이가 거의 없는 것을 확인할 수 있습니다.

3.3 Anomaly detection on MVTec AD

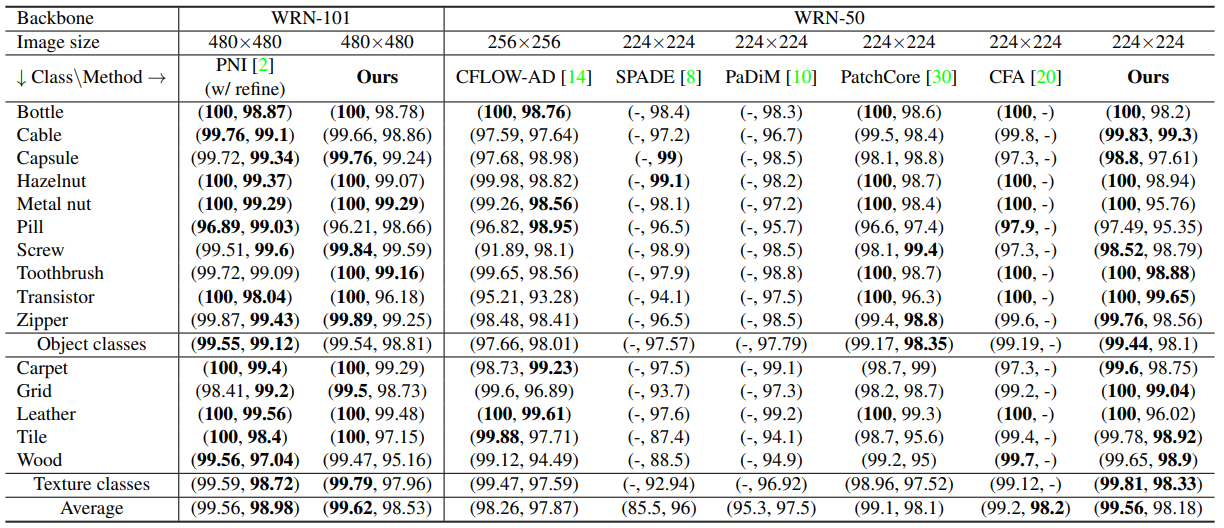
  • single 모델 실험 결과
    • pixel-level AUROC
      • ReConPatch는 anomaly detection 성능을 향상시키는 것에 중점을 둔 모델로, segmentation 성능은 anomaly detection 성능만큼 높지 않을 수 있습니다.
      • 하지만 PatchCore보다는 높은 segmentation 성능을 보였습니다. ReConPatch가 PatchCore의 feature extractor를 수정 및 보완한 모델임을 고려할 때, ReConPatch의 feature extractor가 segmentation 성능 향상에 기여했다고 볼 수 있습니다.
    • image-level AUROC
      • [Backbone WRN-50] 평균 99.56%로 비교 대상 모델들 중에서 가장 높은 성능을 보였습니다.
      • [Backbone WRN-101] 평균 99.62%로 PNI보다 높은 성능을 보였습니다.

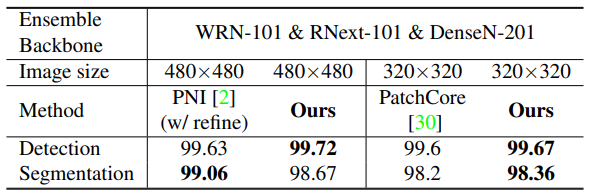
  • ensemble 모델 실험 결과
    • pixel-level AUROC
      • [image size $480\times480$] PNI의 99.06%보다는 낮은 segmentation 성능을 보였습니다.
      • [image size $320\times320$] 평균 98.36%로 PatchCore의 98.2%보다는 높은 segmentation 성능을 보였습니다.
    • image-level AUROC
      • [image size $480\times480$] 99.62 → 99.72 anomaly detection SOTA 성능을 달성했습니다.
      • [image size $320\times320$] 평균 99.67%로 PatchCore의 99.6%보다 더 좋은 성능을 보였습니다. image size를 줄였는데도 PNI가 $480\times480$으로 기록한 성능 99.63%보다 나은 성능을 보였습니다.

3.4 Anomaly detection on BTAD

  • 실험 셋팅
    • feature extractor: pre-trained WideResNet-101
    • image size: $480\times480$
  • 실험 결과
    • [image-level AUROC] 평균 95.8%로 anomaly detection SOTA 성능을 달성했습니다.
    • [pixel-level AUROC] 평균 97.5%로 PatchCore의 97.3%보다 나은 성능을 보였습니다.

3.5 Qualitative analysis

  • ReConPatch가 patch representation을 학습하는 방식의 영향력을 측정하기 위해, UMAP을 이용해 고차원의 patch feature를 2차원 상에 매핑시킨 결과인데요. 가까이 위치한 patch들의 feature가 모여있는 것을 확인할 수 있습니다.
  • 저자들의 주장에 따르면, ReConPatch의 성능 향상은 위 결과에서 볼 수 있듯이 모델이 위치 정보를 학습했기 때문이라고 합니다.
Vision
Anomaly-Detection ReConPatch
This post is licensed under CC BY 4.0 by the author.