[Paper Review] Prototypical Networks for Few-shot Learning

지난 포스트에 이어서 nueral network를 사용한 메트릭 기반 meta learning에 대해 알아보겠습니다. 오늘 소개할 Prototypical Networks(2017)는 단순하지만 강력한 성능을 보여주는 모델입니다. 이름처럼 각 클래스별 prototype 을 계산하여 새로운 샘플이 어떤 클래스에 속하는지를 판단하는 방식을 사용합니다.

1. 학습 진행 과정

1-1. N-way K-shot task 구성

$N$개의 클래스를 랜덤으로 뽑고, 각 클래스마다 $K$개의 support 샘플을 선택합니다.

1-2. Prototype 계산

Support set $S_k$가 주어질 때, 클래스 $k$의 prototype $c_k$는 아래처럼 구합니다.

\[\mathbf{c}_k = \frac{1}{|S_k|} \sum_{\mathbf{x}_i \in S_k} f_\phi(\mathbf{x}_i)\]

각 샘플들의 embedding vector를 구할 때 사용되는 함수 $f(\cdot)$가 바로 neural network입니다. 즉, 클래스별 embedding vector들의 평균을 prototype으로 삼습니다.

1-3. Query 샘플 분류

Query sample $\mathbf{x}$에 대해서는 prototype들과의 거리를 계산하여 softmax로 클래스 확률을 구합니다.

\[p(y=k \mid \mathbf{x}) = \frac{\exp\big(-d\big(f_\phi(\mathbf{x}), \mathbf{c}_k\big)\big)}{\sum_{k'} \exp\big(-d\big(f_\phi(\mathbf{x}), \mathbf{c}_{k'}\big)\big)}\]

여기서 $d(\cdot, \cdot)$은 일반적으로 Euclidean distance를 사용합니다.

\[d(\mathbf{a}, \mathbf{b}) = \| \mathbf{a} - \mathbf{b} \|_2^2\]

1-4. $f(\cdot)$ 파라미터 업데이트

softmax 결과 $p(y=k | \mathbf{x})$와 query 샘플의 정답 레이블 $y$를 비교해서 cross-entropy loss를 계산해서 neural network $f(\cdot)$의 파라미터를 업데이트합니다. 매 episode마다 2~4 과정을 반복하면서 feature extractor $f(\cdot)$는 더 나은 embedding space를 만들도록 학습됩니다.

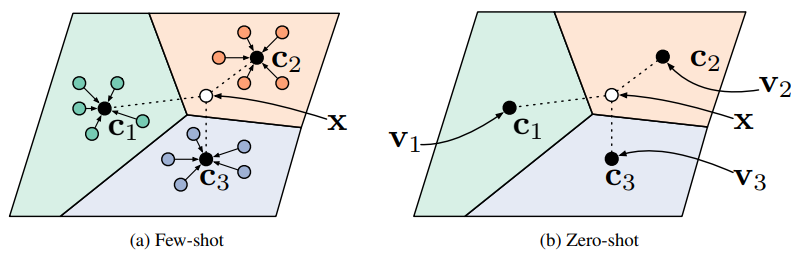Prototypical networks in the few-shot and zero-shot scenarios.

2. Euclidean distance를 사용한 이유

Euclidean distance와 Cosine similarity는 주어진 vector들 사이의 유사도를 계산할 떄 많이 사용되는 방법입니다.

• Cosine similarity
  • 두 벡터의 방향(angle)이 얼마나 유사한지 보는 지표
  • 크기는 무시하고 각도만 비교

\[\text{cosine similarity}(a,b)=\frac{a \cdot b}{||a|| \cdot ||b||}\]

• Euclidean distance
  • 두 벡터 간의 직선 거리를 측정
  • 벡터의 크기와 방향 모두 고려

\[\text{Euclidean distance}(a,b)=||a−b||_2\]

저자들의 실험 결과, Euclidean distance가 Cosine similarity보다 훨씬 좋은 성능을 보였다고 합니다.

We find empirically that the choice of distance is vital, as Euclidean distance greatly outperforms the more commonly used cosine similarity. On several benchmark tasks, we achieve state-of-the-art performance.

저자들이 설명하는 이유는 다음과 같습니다. 첫번째로, Euclidean distance를 쓰면 feature들이 feature space에서 선형 경계로 잘 나뉘도록 학습됩니다. cosine similarity는 방향만 고려하고 magnitude 정보는 무시하므로, 각도는 가깝지만 magnitude가 다른 샘플끼리도 같은 클래스로 분류될 위험이 있습니다.

두번째로, Euclidean distance가 softmax에 바로 입력되기 때문에 gradient 계산이 안정적입니다. Cosine similarity는 normalize 연산이 들어가서 gradient 흐름이 더 복잡해질 수 있습니다.

3. 장점과 한계

Prototypical Networks는 매우 단순한 구조로 이루어져 있기 때문에 구현이 쉽고 계산이 효율적이라는 장점이 있습니다. 하지만 각 클래스가 prototype으로 잘 대표될 수 있어야 좋은 성능을 보장할 수 있습니다. 따라서 intra-class variance가 큰, 같은 클래스 안에서 데이터가 다양하게 퍼져있는 경우에는 적합하지 않을 수있습니다.