Variational Autoencoder(VAE)
본 포스트에서는 GAN에 대해 알아보기에 앞서, GAN과 같은 생성 모델의 일종인 Variational Autoencoder(VAE)에 대해서 다뤄보려고 합니다. 생성 모델은 실존하지는 않지만 현실에 존재할 법한 새로운 데이터를 생성하는 모델인데요. classification 모델처럼 클래스를 구분짓는 decision boundary를 학습하는 것이 아니라 클래스의 확률 분포를 학습합니다. VAE와 깊이 연관된 모델인 Autoencoder에 대해서 먼저 알아보겠습니다.
1. Autoencoder
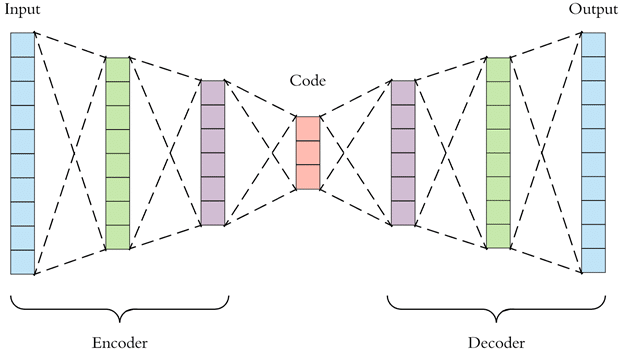
Autoencoder는 encoder과 decoder로 구성된 모델이며, input과 output이 동일합니다. 고차원의 input을 저차원으로 압축했다가 다시 원래 input으로 복원하는 과정을 거칩니다. loss function으로는 input과 output 사이의 Recontruction Error를 사용합니다. 이 loss function을 최소화하기 위해 저차원으로 압축한 feature(code)가 핵심적인 정보를 담도록 학습됩니다. 즉, Autoencoder의 목적은 새로운 데이터를 생성하는 것이 아니라 차원 축소(manifold learning)입니다.
Manifold learning
manifold learning은 고차원 데이터를 저차원에 매핑하는 차원 축소 방법입니다. 차원 축소 기법은 데이터를 선형 공간에 매핑하는지, 비선형 공간에 매핑하는지에 따라 아래와 같이 분류할 수 있는데요.
- 선형
- PCA
- LDA
- 비선형
- Autoencoder
- t-SNE
- LLE
- Isomap
- Kernel PCA
선형 차원 축소 기법은 데이터를 선형 공간에 projection 하여 차원을 축소하는 반면, manifold learning은 비선형 구조를 찾고자 합니다. 따라서 데이터가 본질적으로 비선형 구조를 가질 때 선형 차원 축소 기법보다 manifold learning이 더 효과적일 수 있습니다. manifold를 잘 찾았다면, manifold 좌표들이 조금씩 변할 때 데이터도 유의미하게 조금씩 변하는 것을 확인할 수 있습니다.
2. Variational Autoencoder
앞서 설명한 바와 같이, VAE는 생성 모델의 일종으로 Autoencoder와는 목적이 다릅니다. VAE는 실제 데이터 분포를 잘 학습해서 진짜처럼 보이는 새로운 데이터를 생성할 수 있는 probabilistic decoder $p_\theta(x \vert z)$를 얻고자 합니다. 이를 위해 probabilistic encoder $q_\theta(z \vert x)$를 통해 input $x$를 분포로 매핑합니다. 앞서 Autoencoder의 encoder가 input을 고정된 vector로 매핑했던 것과는 다릅니다.
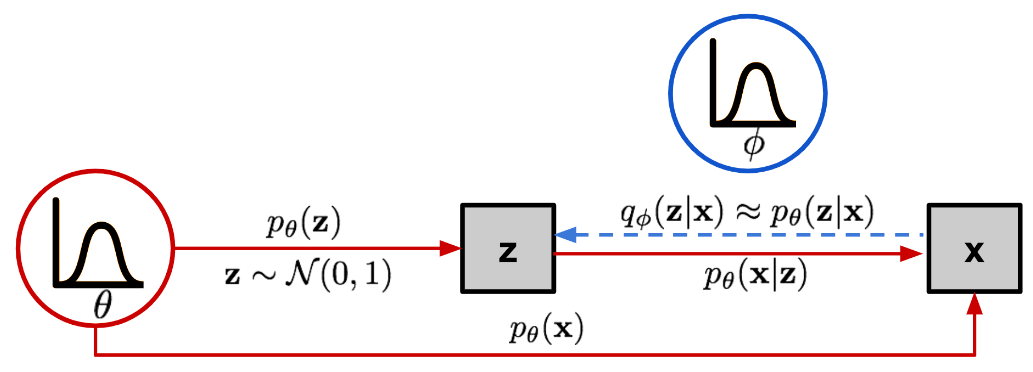
이제부터 Autoencoder와 VAE가 구체적으로 어떤 차이점을 갖는지, decoder $p_\theta(x \vert z)$를 어떻게 학습시킬 수 있는지 알아보도록 하겠습니다. 먼저, input을 $x$라 하고 latent vector를 $z$라 하면 둘 사이의 관계는 다음과 같이 나타낼 수 있습니다.
- 사전 확률 $p_{\theta}(z)$
- Likelihood $p_{\theta}(x \vert z)$
- 사후 확률 $p_{\theta}(z \vert x)$
input $x$와 latent vector $z$의 joint distribution $p(x,z)$에서 $x$의 marginal distribution $p(x)$를 구하려면 가능한 모든 $z$에 대해 $p(x,z)$를 적분해야 합니다. $p(x,z)=p_{\theta}(z)p_{\theta}(x \vert z)$이므로, 최적의 파라미터 $\theta^\ast$는 training data의 likelihood $p_{\theta}(x)=\int{p_{\theta}(z)p_{\theta}(x \vert z)}dz$를 최대화하는 파라미터입니다. 최적의 파라미터 $\theta^\ast$를 구했다고 가정하면, 아래와 같은 순서를 따라 새로운 데이터 $x$를 생성할 수 있습니다.
- 사전 확률 $p_{\theta^*}(z)$에서 $z^{(i)}$를 샘플링
- 조건부 확률 $p_{\theta^*}(x \vert z=z^{(i)})$에서 real data point처럼 보이는 $x^{(i)}$를 생성
하지만 현실적으로 모든 $z$에 대해서 $p_{\theta}(z)p_{\theta}(x \vert z)$를 계산해서 더하는 것은 너무 많은 비용이 듭니다. 사후 확률 $p_{\theta}(z \vert x)=p_{\theta}(x \vert z)p_{\theta}(z)/p_{\theta}(x)$도 계산하는 것이 불가능합니다. 이러한 문제를 해결하기 위해 VAE는 variational inference 방법을 사용합니다. variational inference는 사후 확률 분포를 직접 계산하는 대신, 더 간단한 형태의 분포로 사후 확률을 근사시키는 방법입니다. 즉, 새로운 함수 $q_{\phi}(z \vert x)$를 도입해 $p_{\theta}(z \vert x)$에 근사시켜 문제를 해결하는 것입니다. 여기에서 $q_{\phi}(z \vert x)$가 encoder이고, $p_{\theta}(x \vert z)$가 decoder입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Encoder(nn.Module):
def __init__(self, input_dim, hidden_dim, latent_dim):
super(Encoder, self).__init__()
self.FC_input = nn.Linear(input_dim, hidden_dim)
self.FC_input2 = nn.Linear(hidden_dim, hidden_dim)
self.FC_mean = nn.Linear(hidden_dim, latent_dim)
self.FC_var = nn.Linear (hidden_dim, latent_dim)
self.LeakyReLU = nn.LeakyReLU(0.2)
self.training = True
def forward(self, x):
h_ = self.LeakyReLU(self.FC_input(x))
h_ = self.LeakyReLU(self.FC_input2(h_))
# encoder produces mean and log of variance
# i.e., parateters of simple tractable normal distribution "q"
mean = self.FC_mean(h_)
log_var = self.FC_var(h_)
return mean, log_var
class Decoder(nn.Module):
def __init__(self, latent_dim, hidden_dim, output_dim):
super(Decoder, self).__init__()
self.FC_hidden = nn.Linear(latent_dim, hidden_dim)
self.FC_hidden2 = nn.Linear(hidden_dim, hidden_dim)
self.FC_output = nn.Linear(hidden_dim, output_dim)
self.LeakyReLU = nn.LeakyReLU(0.2)
def forward(self, x):
h = self.LeakyReLU(self.FC_hidden(x))
h = self.LeakyReLU(self.FC_hidden2(h))
x_hat = torch.sigmoid(self.FC_output(h))
return x_hat
Loss Function
$q_{\phi}(z \vert x)$를 $p_{\theta}(z \vert x)$에 근사시키는 것은 곧 $q_{\phi}(z \vert x)$가 $p_{\theta}(z \vert x)$에 최대한 가깝도록 만드는 것입니다. 따라서, 다음과 같이 두 분포 사이의 거리를 측정하는 KL divergence를 사용해 \(D_{KL}(q_{\phi}(z \vert x) \vert\vert p_{\theta}(z \vert x))\)를 최소화하는 문제로 바꿀 수 있습니다.
\[\begin{align*}D_{KL}(q_{\phi}(z|x) \vert\vert p_{\theta}(z|x)) &= \int q_{\phi}(z|x) \log \frac{q_{\phi}(z|x)}{p_{\theta}(z|x)} dz \\ &= \int q_{\phi}(z|x) \log \frac{q_{\phi}(z|x)p_{\theta}(x)}{p_{\theta}(z,x)} dz \\ &= \int q_{\phi}(z|x) \log \frac{p_{\theta}(x|z) q_{\phi}(z|x)}{p_{\theta}(z,x)} dz \\ &= \log p_{\theta}(x) + \int q_{\phi}(z|x) \log \frac{q_{\phi}(z|x)}{p_{\theta}(z,x)} dz \\ &= \log p_{\theta}(x) + \int q_{\phi}(z|x) \log \frac{q_{\phi}(z|x)}{p_{\theta}(x|z)p_{\theta}(z)} dz \\ &= \log p_{\theta}(x) + E_{z \sim q_{\phi}(z|x)} \left[ \log \frac{q_{\phi}(z|x)}{p_{\theta}(z)} - \log p_{\theta}(x|z) \right] \\ &= \log p_{\theta}(x) + D_{KL}(q_{\phi}(z|x) \vert\vert p_{\theta}(z)) - E_{z \sim q_{\phi}(z|x)} \left[ \log p_{\theta}(x|z) \right] \end{align*}\]위 수식의 결과를 정리해보면 다음과 같습니다.
\[\log p_{\theta}(x) - D_{KL}(q_{\phi}(z|x) \vert\vert p_{\theta}(z|x)) = \mathbb{E}_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)] - D_{KL}(q_{\phi}(z|x) \vert\vert p(z))\]위 수식의 좌변은 VAE 학습 과정에서 최대화하고자 하는 것입니다. 관찰된 데이터 $x$가 모델에 의해 생성될 log likelihood $\log p_{\theta}(x)$는 최대화하고자 하고, $q_{\theta}(z \vert x)$와 $p_{\theta}(z \vert x)$ 사이의 거리 \(D_{KL}(q_{\theta}(z \vert x) \vert\vert p_{\theta}(z \vert x))\)는 최소화하고자 하기 때문입니다. 따라서 위 수식에 음수를 취해 loss function으로 사용합니다.
\[\begin{align*}L_{VAE}(\theta, \phi) &= -\log p_{\theta}(x) + D_{KL}(q_{\phi}(z|x) \vert\vert p_{\theta}(z|x)) \\ &= -\mathbb{E}_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)] + D_{KL}(q_{\phi}(z|x) \vert\vert p(z))\end{align*}\]Variational Bayesian 방법론에서 이 loss function은 ELBO(evidence lower bound)로 알려져 있습니다. 이름에 lower bound가 사용된 이유는 KL divergence가 항상 0 이상의 값을 가지기 때문에 $-L_{VAE}$가 $\log p_{\theta}(x)$의 lower bound가 되기 때문입니다.
\[-L_{VAE} = \log p_{\theta}(x) - D_{KL}(q_{\phi}(z|x) \vert\vert p_{\theta}(z|x)) \leq \log p_{\theta}(x)\] \[\begin{align*}\log p_{\theta}(x) &= \log \int p_{\theta}(x,z) dz \\ &= \log \int q_{\phi}(x \vert z) \frac{p_{\theta}(x,z)}{q_{\phi}(x \vert z)} dz \\ &\ge \int q_{\phi}(x \vert z) \log\frac{p_{\theta}(x,z)}{q_{\phi}(x \vert z)} dz \\ &\ge \int q_{\phi}(x \vert z) \log p_{\theta}(x,z) - q_{\phi}(x \vert z) \log q_{\phi}(x \vert z) dz \\ &\ge \int q_{\phi}(x \vert z) \log p_{\theta}(x \vert z)p_{\theta}(z) - q_{\phi}(x \vert z) \log q_{\phi}(x \vert z) dz \\ &\ge \int q_{\phi}(x \vert z) \{\log p_{\theta}(x \vert z)+\log p_{\theta}(z)\} - q_{\phi}(x \vert z) \log q_{\phi}(x \vert z) dz \\ &\ge \int q_{\phi}(x \vert z)\log p_{\theta}(x \vert z) + q_{\phi}(x \vert z)p_{\theta}(z) - q_{\phi}(x \vert z) \log q_{\phi}(x \vert z) dz \\ &\ge \int q_{\phi}(x \vert z)\log p_{\theta}(x \vert z) - q_{\phi}(x \vert z)\log \frac{q_{\phi}(x \vert z)}{p_{\theta}(z)} dz \\ &\ge E_{z \sim q_{\phi}(z|x)} \left[ \log p_{\theta}(x|z) \right] - D_{KL}(q_{\phi}(z|x) \vert\vert p_{\theta}(z)) \\ \end{align*}\]위 식을 다시 써보면 아래와 같이 나타낼 수 있습니다.
\[\text{ELBO}(\phi)=\mathbb{E}_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)] - D_{KL}(q_{\phi}(z|x) \vert\vert p(z)) \leq \log p_{\theta}(x)\] \[L_{VAE}(\theta, \phi) = -\mathbb{E}_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)] + D_{KL}(q_{\phi}(z|x) \vert\vert p(z))\]ELBO는 모델이 데이터를 얼마나 잘 재현할 수 있는지를 나타내는 지표로, 이 값이 높을수록 모델이 실제 데이터 분포를 더 정확히 학습했다고 볼 수 있습니다. ELBO를 최대화하는 것은, 결과적으로 $\log p_{\theta}(x)$를 최대화하는 것으로 이어지며, 이는 데이터를 잘 생성하는 모델의 성능을 의미합니다.
VAE에서 loss function $L_{VAE}(\theta, \phi)$은 ELBO를 최대화하는 방향으로 $\theta$와 $\phi$를 업데이트함으로써, 궁극적으로 생성된 데이터의 log likelihood를 최대화합니다. $L_{VAE}(\theta, \phi)$에서 첫번째 항이 의미하는 것은 Reconstruction Error입니다. latent vector $z$로부터 input $x$를 얼마나 잘 복원하는지 측정하는 데 사용됩니다.
두번째 항은 Regularization 항입니다. encoder의 출력 $q_\phi(z \vert x)$과 사전 확률 $p_{\theta}(z)$ 간의 차이가 작아지도록 함으로써 VAE를 통해 생성된 latent vector $z$가 사전 확률 $p_{\theta}(z)$를 따르도록 강제하는 역할을 하는데요. 이는 앞서 살펴본 Autoencoder에는 없던 제약 조건입니다. Autoencoder는 Reconstruction Error를 최소화하도록 학습할 뿐이고 latent vector $z$가 특정한 분포를 따르지 않습니다. 반면에 VAE에서는 이 Regularization 항을 통해 latent space를 연속적으로 만듭니다. latent space가 연속적이라는 것은 데이터를 변형하거나 interpolation 할 때 의미있는 결과를 생성할 수 있도록 latent space가 잘 구조화되어 있음을 의미합니다. 임의의 두 vector $z_1$, $z_2$를 interpolation한 vector들을 decoder에 입력해 결과 이미지를 나열해보면, 있을 법한 이미지들이 생성되며 부드러운 transition이 나타나는 것을 확인할 수 있습니다. 이러한 특성은 VAE가 이미지 생성 분야에서 강력한 도구로 활용되는 이유 중 하나입니다.
Reparameterization Trick
VAE의 loss function에서 기댓값을 계산하는 항은 latent vector $z$의 분포로부터 샘플을 뽑는 과정을 포함합니다. 다시 말해, encoder를 통해 input $x$로부터 얻은 분포 $q_\phi(z \vert x)$에서 $z$를 샘플링하여 decoder가 이를 기반으로 데이터를 재구성하고, 그에 대한 loss를 계산합니다. 그런데 샘플링은 확률적 과정(stochastic process)이기 때문에 gradient를 계산할 수 없습니다. 무작위성이 포함되어 있어 동일한 input에도 output이 달라질 수 있으므로, 명확한 함수적 관계를 찾기가 어렵기 때문입니다. VAE에서는 이를 해결하기 위해 Reparameterization Trick을 사용합니다.
VAE에서 input $x$에 대해 encoder가 $z$의 조건부 분포 $q_\phi(z \vert x)$를 모델링합니다. 일반적으로 이 분포는 평균 $\mu$와 분산 $\sigma^2$를 갖는 가우시안 분포로 가정합니다. 즉, encoder는 input $x$로부터 $\mu$와 $\sigma$를 출력합니다. 이 때, Reparameterization Trick을 사용해 $z$를 다음과 같이 표현합니다.
\[z=\mu+\sigma \odot \epsilon\]여기에서 $\epsilon$은 표준 정규 분포에서 샘플링된 노이즈로써, 역전파할 때 gradient 계산에 영향을 주지 않습니다. 이처럼 $z$의 샘플링 과정에서 발생하는 확률적 변동성을 모델의 파라미터 $\mu$와 $\sigma$로 reparameterization함으로써 gradient를 효과적으로 계산하고 역전파할 수 있게 됩니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Model(nn.Module):
def __init__(self, Encoder, Decoder):
super(Model, self).__init__()
self.Encoder = Encoder
self.Decoder = Decoder
def reparameterization(self, mean, var):
# reparameterization trick
# sampling epsilon
epsilon = torch.randn_like(var).to(DEVICE)
z = mean + var*epsilon
return z
def forward(self, x):
mean, log_var = self.Encoder(x)
# takes exponential function (log var -> var)
z = self.reparameterization(mean, torch.exp(0.5 * log_var))
x_hat = self.Decoder(z)
return x_hat, mean, log_var
VAE는 explicit likelihodd function을 최적화려고 하다보니 low bound에 대한 최적화에 그친다는 한계가 있습니다. 다음 포스트에서 다룰 예정인 GAN은 VAE와 달리 implicit distribution을 모델링하는, likelihood-free 모델입니다.