[Paper Review] ArcFace: Additive Angular Margin Loss for Deep Face Recognition

이번 포스트에서는 얼굴 인식 분야에서 큰 주목을 받은 모델 중 하나인 ArcFace(2019)에 대해 알아보겠습니다. ArcFace는 얼굴 인식에서 margin-based softmax loss를 이용해 기존보다 훨씬 높은 분류 성능과 discriminative power를 달성한 모델로 평가받고 있습니다. ArcFace의 핵심 아이디어는 무엇인지, 그리고 기존 방법과 어떤 차이가 있는지 자세히 살펴보겠습니다.

1. 모델 구조

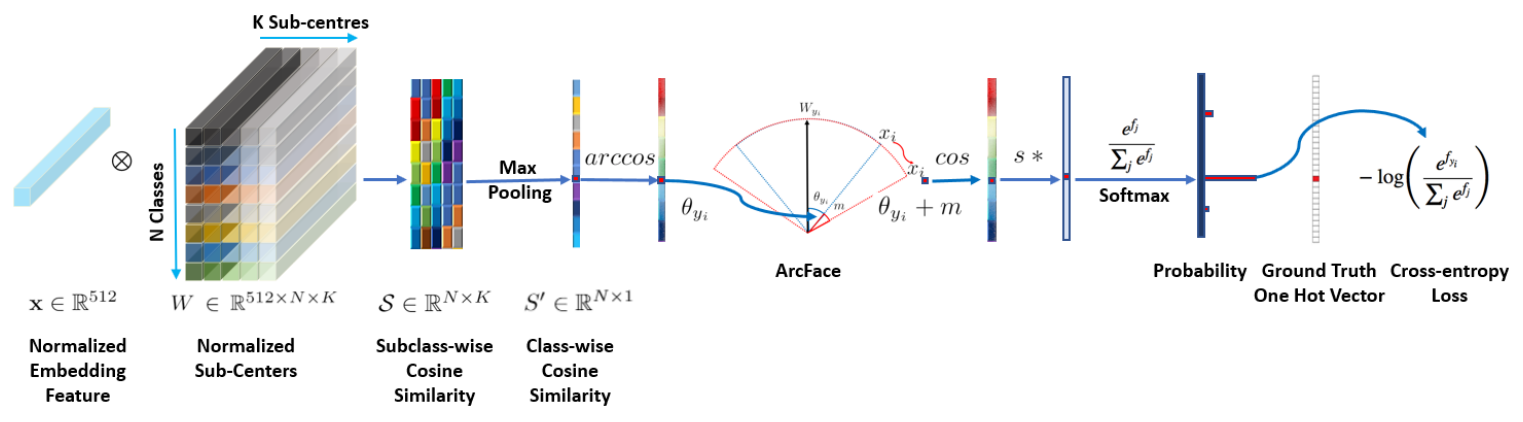
Step 1 Backbone network(ResNet)을 사용해 feature를 추출합니다.

Step 2 feature vector $\mathbf{x}$를 L2 정규화해서 크기가 항상 1인 vector로 만듭니다. 이를 통해 softmax에서 vector의 크기(norm) 대신 각도(angle)로 클래스를 구분할 수 있게 됩니다.

\[\hat{\mathbf{x}} = \frac{\mathbf{x}}{\| \mathbf{x} \|}\]

Step 3 각 class별 weight vector $\mathbf{W}_k$도 L2 정규화합니다.

\[\hat{\mathbf{W}} = \frac{\mathbf{W}}{\| \mathbf{W} \|}\]

Step 4 정규화된 feature vector와 각 class weight 사이의 각도 $\theta$를 구합니다.

\[\cos(\theta_k)=\hat{\mathbf{W}}_k^\top \hat{\mathbf{x}}\]

Step 5 정답 class에만 angular margin $m$을 더합니다.

\[\cos(\theta_y+m)\]

Step 6 각도를 cosine으로 표현하면 값 범위가 $[−1,1]$로 너무 작아져서 gradient가 약해질 수 있기 때문에 scaling factor $s$를 곱합니다.

\[s \cdot \cos(\theta_y+m)\]

Step 7 최종 logit을 softmax에 넣어 cross-entropy loss를 계산합니다.

\[p_y = \frac {e^{s \cdot \cos(\theta_y + m)}} {e^{s \cdot \cos(\theta_y + m)} + \sum_{j \ne y} e^{s \cdot \cos(\theta_j)}}\]

loss는 아래처럼 계산합니다.

\[L=−\log(p_y)\]

Step 8 cross-entropy loss로 gradient 계산해서 Backbone network와 $\mathbf{W}$를 모두 업데이트합니다. 결과적으로 같은 사람끼리는 더 가깝고, 다른 사람끼리는 더 멀어지도록 feature embedding이 학습됩니다.

2. 핵심 아이디어: angular margin

ArcFace의 핵심은 softmax 계산에서 각도($\theta$)에 margin $m$ 을 더하는 것입니다.

• 기존 softmax logits:

\[z_i = \|W_{y_i}\| \cdot \|x_i\| \cdot \cos(\theta_{y_i})\]

• ArcFace의 수정된 logits:

\[z_i = \|x_i\| \cdot \cos(\theta_{y_i} + m)\]

weight와 feature를 L2 정규화하고, $\cos(\theta)$에 margin $m$을 더함으로써 angular decision boundary를 더 넓게 만듭니다.

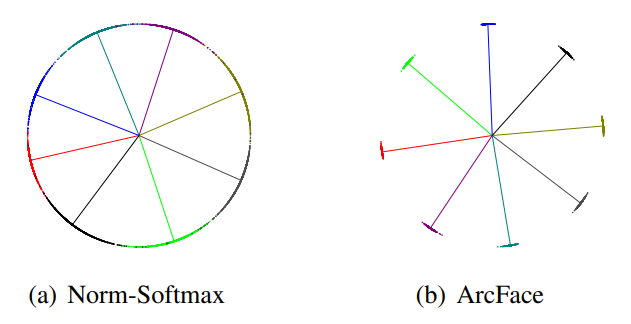
얼굴 인식의 핵심은 같은 사람은 feature space에서 가깝고, 다른 사람은 멀리 배치하는 것입니다. 하지만 기존 softmax(a)는 feature 간의 각도를 충분히 구분하지 못해 decision boundary가 명확하지 않다는 문제가 있었습니다. ArcFace(b)는 여기에 angular margin을 추가해 같은 클래스는 더 촘촘히 모이고, 다른 클래스는 더 멀어지도록 유도하여 구분력을 극적으로 높였습니다.

3. Implementation Details

저자들의 주장에 따르면 ArcFace를 구현할 때 중요한 세팅은 아래와 같습니다.

• feature와 weight vector는 L2-normalization으로 크기를 1로 고정
• scaling factor $s$를 사용해서 gradient의 magnitude를 조절
• margin $m$이 너무 크면 overfitting 위험이 있으므로 tuning

4. FaceNet과의 차이점

지난 포스트에서 살펴본 FaceNet과의 차이점을 정리해보면 아래와 같습니다. 두 모델 모두 metric learning의 일종이지만 접근 방식이 다릅니다.

구분	FaceNet	ArcFace
접근 방식	distance-based	classification-based
Loss	Triplet Loss	Margin-based Softmax Loss
학습 단위	Triplet (anchor, positive, negative)	하나의 sample
Class label 활용	간접적	직접적
목적	embedding 거리 직접 학습	Softmax decision boundary 개선