[Paper Review] PaDiM: a Patch Distribution Modeling Framework for Anomaly Detection and Localization

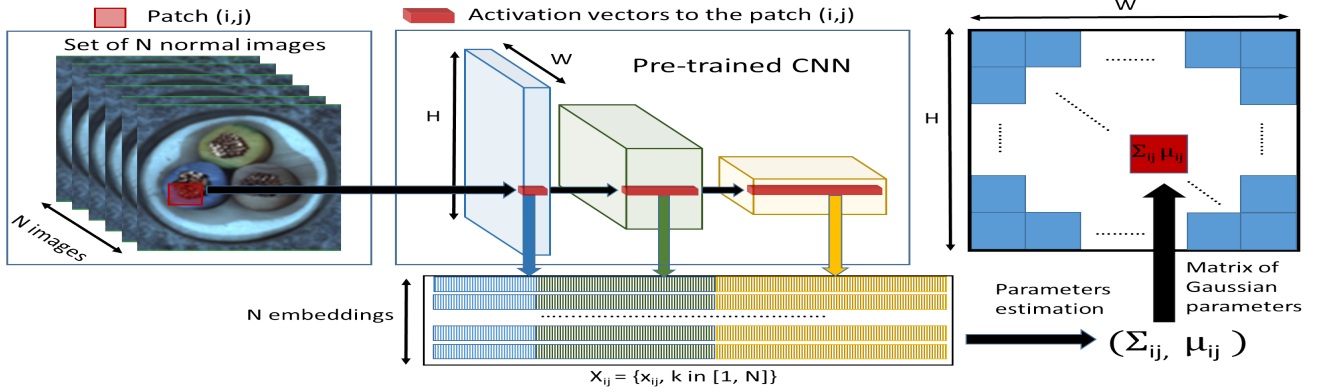
PaDiM은 이미지를 patch 단위로 쪼개어 분석하는 모델입니다. pre-trained CNN model을 사용해서 각각의 patch에 해당하는 embedding vector를 생성하고, 이 embedding vector를 통해 각각의 patch를 multivariate Gaussian ditribution으로 표현하는 것이 PaDiM의 차별점입니다. 본 포스트에서는 PaDiM이 이상탐지를 진행하는 구체적인 과정과 함께 MVTec 데이터셋으로 모델 성능을 평가한 결과를 살펴보겠습니다.

이상탐지 진행 과정

PaDiM 이상탐지 진행 과정

1. Embedding extraction

위 이미지의 가운데에서 patch의 embedding vector를 만드는 과정을 설명하고 있는데요, PaDiM에서 embedding vector를 만드는 방식은 SPADE와 거의 동일합니다. pre-trained CNN 모델의 각기 다른 layer에서 patch feature를 추출하고, 이 feature들을 합쳐서 patch embedding vector를 만듭니다. 이미지에서는 생략되었지만, 각기 다른 layer에서 추출한 feature map들은 크기가 다르기 때문에 bicubic interpolation을 통해 크기를 맞춰준 다음 concatenate 합니다.

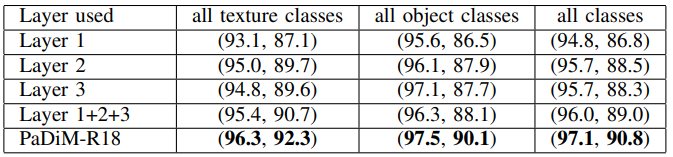
이러한 방식으로 만들어진 embedding vector는 서로 다른 semantic level과 resolution으로부터 나온 정보를 포함하고 있어서 localization 성능을 향상시킵니다. 위 표에 따르면 layer 각각의 output을 patch embedding vector로 사용(Layer 1, Layer 2, Layer 3)했을 때보다 세 개의 output을 합쳤을 때(Layer 1+2+3) anomaly localization 성능이 더 높습니다. 그리고 모든 위치의 patch를 multivariate Gaussian distribution으로 표현해서 layer output 간의 상관관계를 함께 고려했을 때(PaDiM-R18) 성능이 가장 높다는 것을 확인할 수 있습니다.

정상 이미지 $N$개의 embedding vector들의 집합 $X_{ij}$는 아래와 같이 표현할 수 있습니다. 여기에서 $ij$는 patch의 위치를 의미합니다.

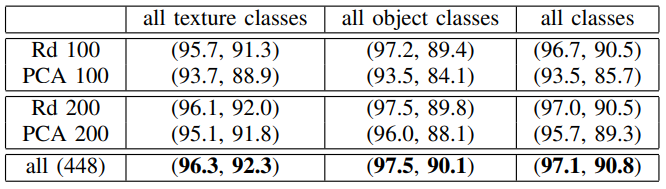
\[X_{ij}=\{ {x_{ij}}^k, k\in [1, N] \}\]

그리고 patch embedding vector가 불필요한 정보를 포함하고 있을 수 있기 때문에 차원축소 과정을 거칩니다. 저자들의 실험에 따르면, 단순히 일부 dimension을 랜덤하게 선택(Rd)하면 성능은 유지하면서 PCA보다 더 효율적으로 차원을 축소할 수 있다고 합니다. 위 표는 차원축소 없이 모든 dimension을 사용한 결과(all)와 차원축소를 거친 결과(Rd, PCA)의 차이를 보여줍니다.

2. Learning of the normality

다음 단계는 이미지 내 모든 위치 $(i, j)$에서 정상 이미지의 특성을 학습하는 것입니다. $X_{ij}$가 multivariate Gaussian distribution $\mathcal{N}(\mu_{ij}, \sum_{ij})$을 따른다고 가정합니다. $\mu_{ij}$는 $X_{ij}$의 표본 평균이고, $\sum_{ij}$는 $X_{ij}$의 표본 공분산입니다.

\[\sum_{ij}=\frac{1}{N-1}\displaystyle\sum_{k=1}^N(x_{ij}^k-\mu_{ij})(x_{ij}^k-\mu_{ij})^T+\varepsilon I\]

모든 위치에서 Gaussian parameter를 구하면 위 이미지의 오른쪽에서 보이는 것처럼 Gaussian parameter의 matrix를 구성할 수 있습니다.

3. Inference: computation of the anomaly map

마지막 단계는 anomaly map을 구하는 단계입니다. 테스트 이미지의 patch embedding $x_{ij}$와 학습한 분포 $\mathcal{N}(\mu_{ij}, \sum_{ij})$ 사이의 마할라노비스 거리를 구합니다. 이 값이 크다는 것은 정상 분포와 거리가 멀다는 의미이므로, 해당 patch는 비정상이라고 볼 수 있습니다. 모든 위치에 대해 거리를 구하면 마할라노비스 matrix $M$을 구성할 수 있고, 이 matrix가 곧 anomaly map입니다. 최종적으로 전체 이미지의 anomaly score는 $M$의 최댓값을 사용합니다.

모델 성능 평가

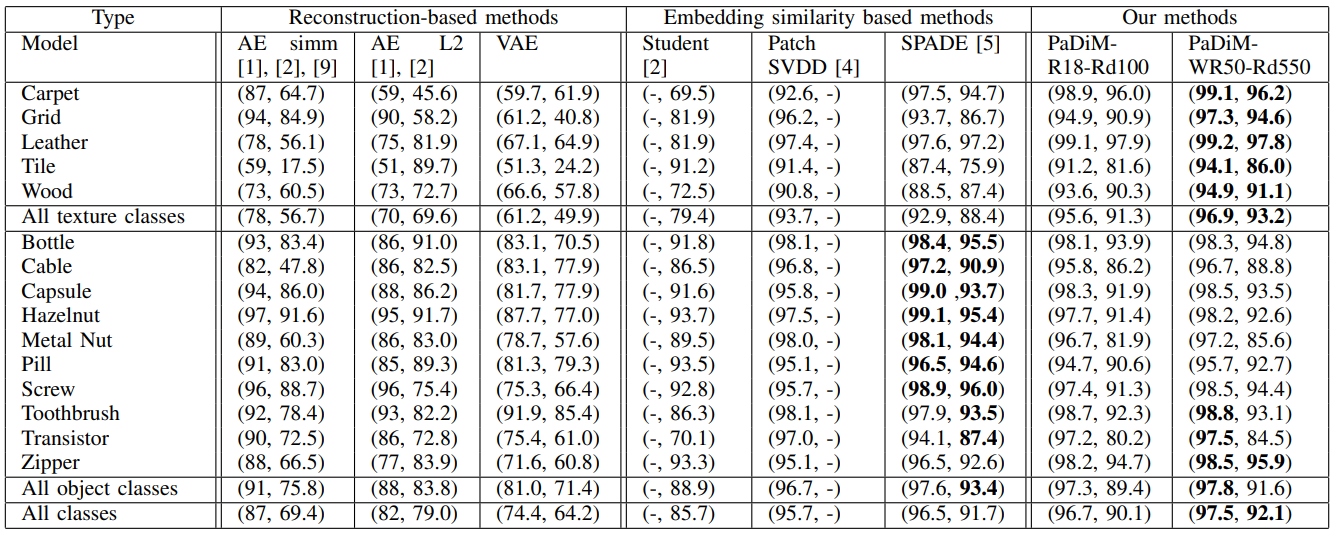
PaDiM은 texture class에서 높은 성능을 보였습니다. 반면에, object class에서는 SPADE보다 낮은 성능을 보였는데요. 이는 PaDiM이 각각의 위치에서 정상 이미지 전체를 관통하는 통계적 유사성을 효과적으로 잡아내는 특징이 있기 때문입니다.

위 이미지는 실험에 사용된 MVTec dataset의 이미지 중 일부입니다. texture class는 특정 패턴을 보여주기 때문에 이미지 alignment가 성능에 큰 영향을 주지 않습니다. 그래서 PaDiM을 사용했을 때 높은 성능을 얻을 수 있습니다. 하지만 object class의 경우, 만약 물체가 정렬되어 있지 않거나 중앙에 위치해 있지 않으면 위치별 multivariate Gaussian distribution을 구하는 PaDiM의 특성상 성능이 크게 저하될 것입니다. 반면 SPADE는 이미지 내 특정 pixel과 $K$개 최근접 이웃 이미지들의 모든 pixel 사이의 거리를 산출하기 때문에 이미지 alignment에 덜 의존적이라는 장점을 갖습니다.

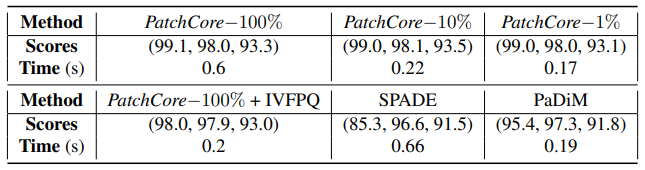Mean inference time per image on MVTec AD. Scores are (image AUROC, pixel AUROC, PRO metric)

PatchCore 저자들의 실험을 정리한 위 표에 따르면, 동일한 MVTec dataset에 대해 PaDiM은 SPADE보다 inference 속도가 빠르고, 성능도 더 우수합니다. 또한 전체 중 10%의 coreset을 subsampling한 PatchCore-10%보다 성능은 낮지만 inference 속도가 빠르다는 점을 확인할 수 있습니다.

한계점

• PaDiM은 K nearest neighbor 방법을 사용하지는 않지만, 정상 이미지의 분포를 학습하는 과정에서 공분산 행렬을 구해야 하는데 이 과정에서 많은 연산량이 필요합니다.
• 이미지 내 각각의 위치에서 정상 이미지 전체를 관통하는 multivariate Gaussian distribution을 구하기 때문에 이미지 alignmnet에 의존적이고, train과 test 시에 이미지 shape이 동일해야 합니다.