[Paper Review] Sub-Image Anomaly Detection with Deep Pyramid Correspondences
K-nearest neighbor 방식은 이미지 자체가 정상인지 혹은 비정상인지는 잘 판단하지만, 이미지 내 어느 부분이 비정상인지를 잘 설명하지 못합니다. 본 논문에서는 이러한 한계점을 극복하기 위해 Gallery 라는 개념을 사용합니다. Gallery는 정상 이미지의 pixel feature들을 저장해두는 일종의 저장소인데요. Gallery에 저장해둔 정상 이미지의 pixel feature들과 비정상 이미지의 pixel feature들 사이의 Euclidean 거리를 측정해서 anomaly score를 산출하는 것이 핵심 과정입니다. 본 포스트에서는 본 논문에서 제안하는 SPADE 모델의 구조와 성능 평가 결과를 함께 살펴보겠습니다.
이상탐지 진행 과정
1. Feature Extraction
첫 번째 단계는 이미지의 feature를 추출하는 것입니다. SPADE는 ImageNet 데이터로 pre-train한 Wide-ResNet50을 사용하여 이미지의 feature를 추출하는데요. ResNet의 마지막 convolutional layer에서 global pooling을 거친 결과 값을 추출하여 feature로 사용합니다. 별도의 학습을 필요로 하지 않기 때문에 매우 빠를 뿐만 아니라, self-supervised feature learning 방식으로 feature를 처음부터 학습하는 것보다 정확도도 높다고 합니다. 주어진 이미지를 $x_i$, feature extractor를 $F$라고 하면, 추출된 feature $f_i$는 다음과 같이 나타낼 수 있습니다.
\[f_i=F(x_i)\]학습 과정에서는 정상 이미지의 feature만 추출해서 Gallery에 저장해 두고, 추론 과정에서는 테스트 이미지 $y$의 feature만 추출합니다.
2. K Nearest Neighbor Normal Image Retrieval
두 번째 단계는 학습 데이터의 정상 이미지들 중에서 테스트 이미지 $y$와 가장 유사한 $K$개의 이미지를 찾는 단계입니다. 다음 단계에서 sub image level 이상탐지를 수행하기 위한 preseletion 단계라고 볼 수 있습니다. 테스트 이미지 $y$가 주어지면, 먼저 학습 데이터와 같은 방식으로 feature $f_y$를 추출합니다.
\[f_y=F(y)\]그 다음 정상 이미지들 중에서 테스트 이미지 $y$의 feature와 가장 가까운, $K$개의 최근접 정상 이미지 $N_K(f_y)$를 찾습니다. 그리고 최근접 이미지들의 feature와 테스트 이미지 $y$의 feature의 Euclidean 거리 평균 $d(y)$을 구합니다.
\[d(y)=\frac{1}{K}\sum_{f\in{N_K(f_y)}}{||f-f_y||}^2\]$d(y)$가 특정 threshold보다 크면, 즉 테스트 이미지 $y$가 정상 이미지와 거리가 멀면 비정상으로 분류하는데요. 실제 분석 상황에서는 데이터에 따라, 요구되는 미검/과검 성능에 따라 적정 threshold를 유연하게 조정합니다.
3. sub-image Anomaly Detection via Image Alignment
두 번째 단계에서 테스트 이미지 $y$를 비정상으로 분류했다면, 이제 이미지 상에서 어느 부분이 비정상인지 표시할 차례입니다. 만약 이전 단계에서 정상 이미지를 비정상 이미지로 잘못 분류했더라도, 이번 단계에서 어떤 픽셀도 비정상으로 표시되지 않는다면 해당 이미지를 정상으로 재분류할 수 있습니다.
앞서 언급한 Gallery가 이번 단계에서 등장하는데요. 테스트 이미지 $y$의 $K$개 최근접 정상 이미지 $N_K(f_y)$에서 추출했던 feature들로 Gallery $G$를 구성합니다. 이 때, feature는 이미지를 구성하는 모든 pixel $p$로 쪼개어 저장합니다. 마찬가지로 테스트 이미지 $y$의 feature를 구한 다음, 특정 pixel $p$에 해당하는 feature $F(y, p)$를 구해서 Gallery 내 모든 pixel feature와의 Euclidean 거리를 구합니다. 이 거리들 중, 가장 가까운 $\kappa$개 거리의 평균 $d(y, p)$을 구합니다. ($\kappa$는 최근접 이미지의 개수를 의미하는 $K$와는 다릅니다.)
$d(y, p)$는 테스트 이미지 $y$의 특정 pixel $p$의 anomaly score를 의미합니다. 만약 $d(y, p)$가 특정 threshold보다 크다면, 즉 정상 이미지에서 비슷한 pixel feature를 찾지 못했으면 해당 pixel은 비정상으로 표시됩니다. 여기에서 주목할 점은, 테스트 이미지 $y$의 특정 pixel $p$와 $K$개 최근접 이웃 이미지들의 모든 pixel들 사이의 거리가 산출된다는 것입니다. 모든 위치와의 거리를 산출하기 때문에 이미지 alignment에 덜 의존적이라는 장점을 갖습니다.
3-1. Feature Pyramid Matching
세 번째 단계에서 feature를 추출하는 방법은 첫 번째 단계와는 조금 다릅니다. pixel간 비교를 효과적으로 수행하기 위해, Wide-ResNet50 내 여러 단계의 feature를 추출해서 합치는 방법을 사용했습니다. 단계별로 feature map 크기가 다르기 때문에 bilinear interpolation을 거쳐 크기를 맞춰준 다음 concatenate 합니다.
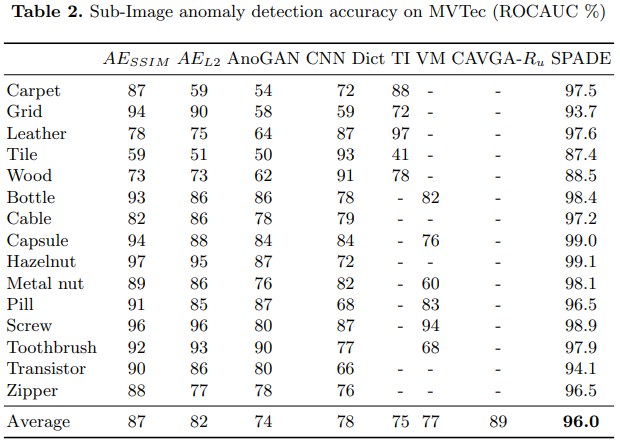
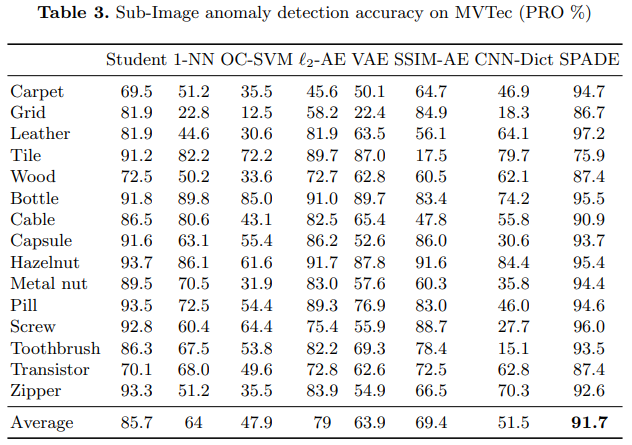
모델 성능 평가
논문에서 실험에 사용한 하이퍼파라미터는 다음과 같습니다.
- (MVTec) $K=50$
- (STC) $K=1$
- $\kappa=1$
한계점
K nearest neighbor(KNN) 방식은 학습 데이터 크기에 비례하여 복잡도가 증가합니다. 모든 데이터 조합의 거리를 구해야 하기 때문인데요. 앞서 설명한 바와 같이, SPADE에서는 image level(두 번째 단계)과 sub image level(세 번째 단계) 이상탐지를 수행할 때 KNN 방식을 사용합니다. sub image level 이상탐지 시에는 이전 단계에서 찾아낸, 고정된 개수의 이미지 $K$개만을 대상으로 pixel feature들 사이의 거리를 구하긴 하지만, image level 이상탐지를 수행할 때는 테스트 이미지 $y$와 학습 데이터에 포함된 모든 정상 이미지들 사이의 거리를 구해야 합니다. 따라서 학습 데이터가 커지면, 그만큼 계산 시간이 많이 소요된다는 한계점이 있습니다.