기계번역 분야에서의 RNN

RNN 모델은 LM뿐만 아니라, NLP 분야의 다양한 task에서 활용되고 있습니다. 이번 포스트에서는 기계 번역(Machine Translation) 분야를 다뤄보고자 합니다.

encoder-decoder

모델 구조

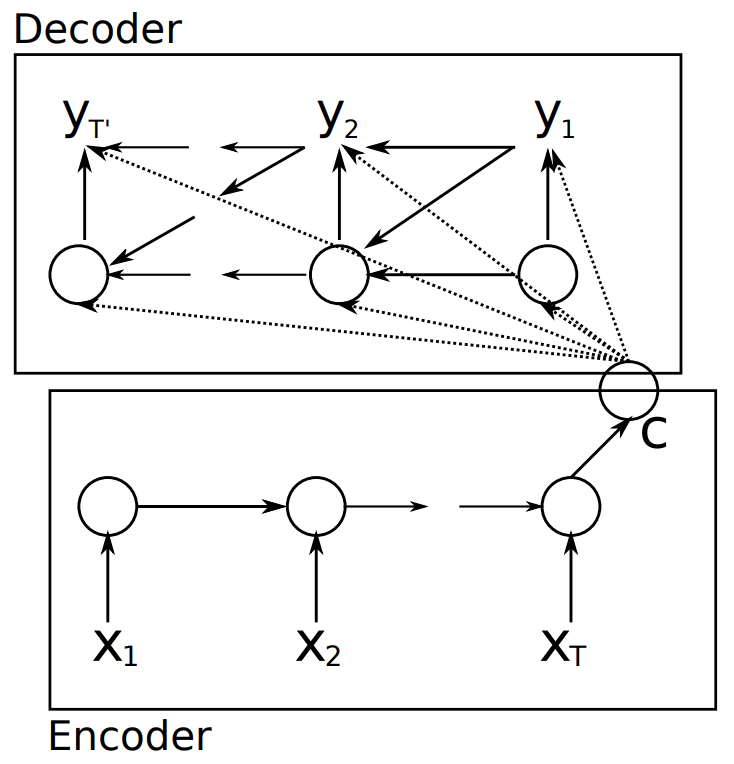
RNN을 사용한 기계 번역 모델의 토대인, 두 개의 RNN으로 구성된 encoder-decoder 모델은 cho et al. 2014에서 제안되었습니다. encoder에서 source sequence를 순서대로 입력받아 고정된 길이의 context 벡터 $C$로 만들고, 이 벡터를 decoder에서 입력받아 target sequence를 생성하는 구조입니다.

encoder와 decoder에서는 time step $t$마다 hidden state $h^{\lt t \gt}$를 다음과 같이 업데이트 합니다.

Encoder:

\[h_{<t>}=f(h_{<t-1>}, x_t)\]

Decoder:

\[h_{<t>}=f(h_{<t-1>}, y_{t-1}, c),\\ c=tanh(Vh^{<N>})\]

여기에서 $f$는 비선형 활성함수, $h^{\lt N \gt}$는 마지막 time step에서 생성되는 hidden state이고, $c$는 input sequence 전체를 대표하는 context 벡터입니다.

결과적으로 encoder와 decoder는 다음과 같이 input sequence가 주어졌을 때 output sequence의 조건부 확률을 최대화 하는 방향으로 학습됩니다.

\[max_{\theta}\frac{1}{N}\sum_{n=1}^{N}logp_{\theta}(y_n|x_n)\]

여기에서 $\theta$는 모델 파라미터이고, $x_n$은 input sequence, $y_n$은 output sequence입니다.

GRU

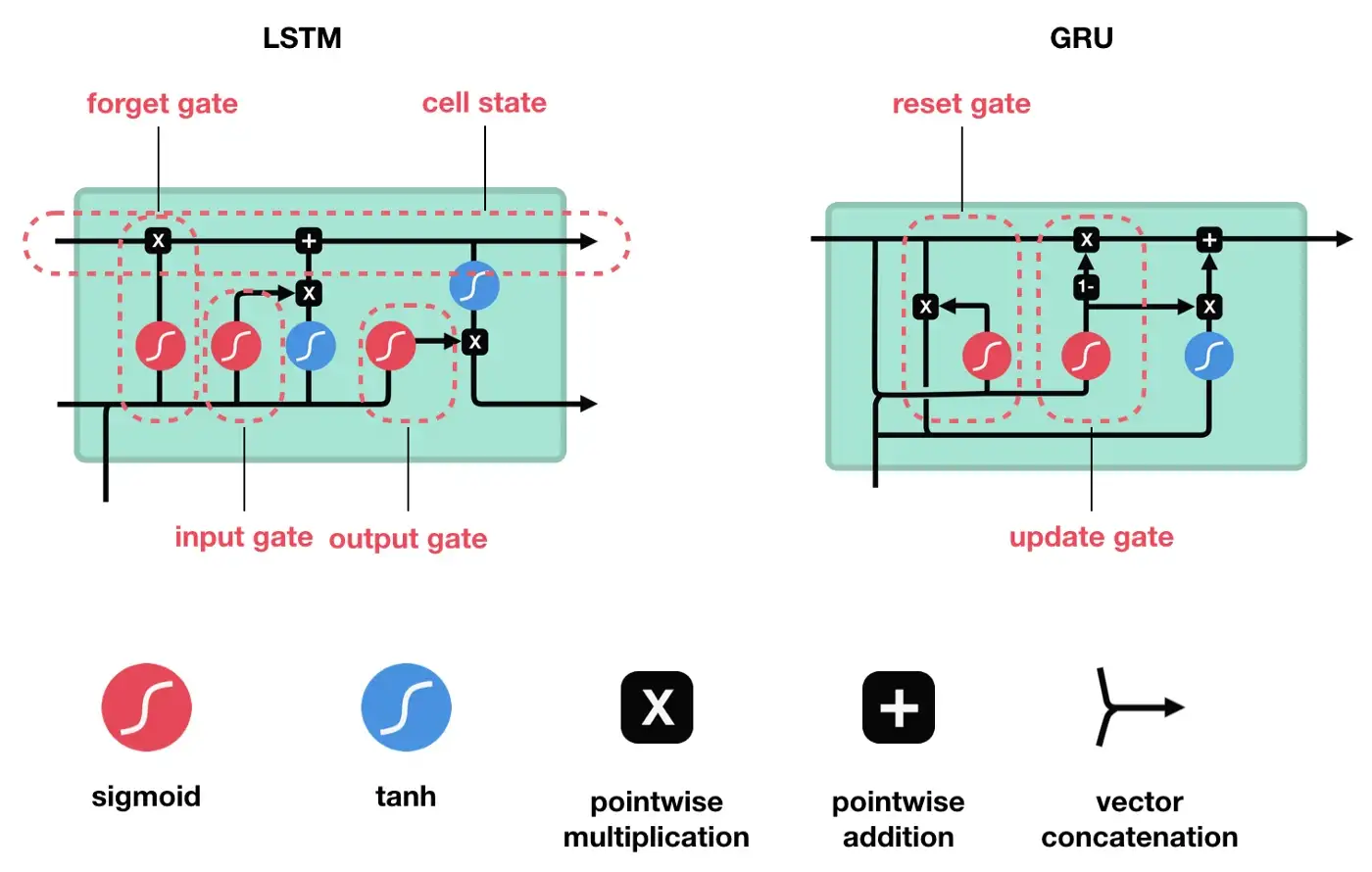
또한 본 논문에서 LSTM의 간소화 버전인 GRU도 제안되었는데요.

reset gate $r_j$와 update gate $z_j$는 다음과 같이 계산됩니다. $x$는 input, $h_{t-1}$는 이전 시점의 hidden state이고, $W$와 $U$는 학습되는 weight matrix입니다. 시그모이드 함수로 인해 gate의 output은 0과 1사이의 값을 가집니다.

\[r_j=\sigma([W_{r}x]_j+[U_{r}h_{<t-1>}]_j)\] \[z_j=\sigma([W_{z}x]_j+[U_{z}h_{<t-1>}]_j)\]

결과적으로 $t$시점의 $j$번째 hidden state는 다음과 같이 계산됩니다.

\[h_j^{<t>}=z_{j}h_{j}^{<t-1>}+(1-z_j)\tilde{h}_j^{<t>}\] \[\tilde{h}_j^{<t>}=\phi([Wx]_j+[U(r \odot h_{<t-1>})]_j)\]

reset gate가 0에 가까워지면 이전 시점의 hidden state $h_j^{\lt t-1 \gt}$을 무시하고 현재 시점의 input $x$로 $\tilde h_j^{\lt t \gt}$를 업데이트합니다. 이 과정에서 관련 없는 정보가 버려지면서 보다 유용한 hidden state를 얻을 수 있습니다. update gate는 이전 시점의 hidden state $h_{t-1}$으로부터 얼마나 많은 정보를 유지할 것인지 결정합니다. 그래서 update gate가 0에 가까워지면 hidden state $h_j^{\lt t \gt}$가 새로운 hidden state $\tilde h_j^{\lt t \gt}$로 업데이트되고, 1에 가까워지면 이전 시점의 hidden state $h_j^{\lt t-1 \gt}$의 정보를 대부분 유지한 상태로 hidden state $h_j^{\lt t \gt}$가 업데이트됩니다. short-term dependency를 잡아내도록 학습되는 unit들은 reset gate가 자주 활성화되고, long-term dependency를 잡아내도록 학습되는 unit들은 update gate가 자주 활성화됩니다.

Attention

등장 배경

위 모델의 한계점은 source sentence의 길이에 관계없이, encoder에서 모든 문맥 정보를 고정된 길이의 context 벡터로 압축해야 한다는 것인데요. Bahdanau et al. 2014는 이러한 구조로 인해 병목현상이 발생하여 모델 성능이 하락한다고 지적합니다. decoder에서 target word를 예측할 때 source sentence의 어떤 부분에 관련 정보가 집중되어 있는지 모델 스스로 찾을 수 있도록 하는 attention 방식을 제안합니다.

모델 구조

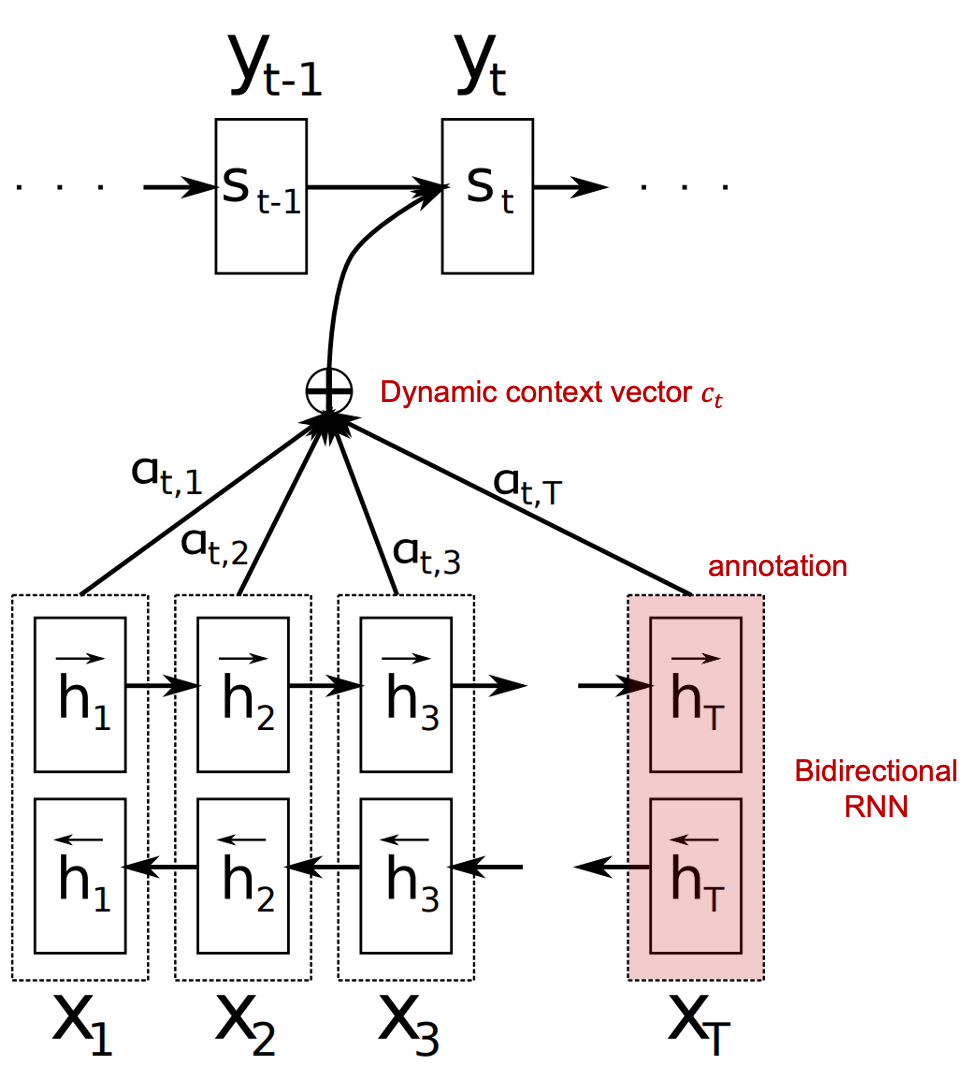
위 그림을 기준으로 설명하면, decoder에서 $s_t$을 출력할 때마다 encoder의 annotation들의 가중합 $c_t=\sum_{j=1}^{T}{\alpha_{tj}h_j.}$을 참고하는 방식입니다.

• annotation $h_j$는 forward hidden states와 backward hidden states를 concatenate한 것입니다.
• attention 가중치 $\alpha$는 이전 시점 decoder의 hidden state $s_{t-1}$와 현재 시점 encoder의 hidden state $h$들 사이의 유사도(energy)를 산출한 다음, 이 유사도에 softmax를 취해서를 구합니다. 예를 들어, dot-product를 이용해 유사도를 산출한다면 계산 과정은 다음과 같습니다.

\[e_{t1}=s_{t-1} \cdot h_1, \\ e_{t2}=s_{t-1} \cdot h_2, \\ ...\\ e_{tT}=s_{t-1} \cdot h_T\\ \alpha_{tj}=\frac{exp(e_{tj})}{\sum_{k=1}^{T}{exp(e_{tk})}}\]

• $c_t$가 cho et al. 2014의 context 벡터와 유사한 역할을 하는 것인데, cho et al. 2014의 context 벡터와 달리 고정되어 있지 않고 time step $t$마다 다르기 때문에 dynamic context 벡터라고 부릅니다.

Attention의 장점 및 한계점

이러한 구조를 사용하면 decoder가 $s_t$를 출력해서 결과적으로 $y_t$를 결정할 때 source sentence의 어느 부분에 집중해야 할지 결정해서 정보를 선택적으로 가져옵니다. 따라서 긴 문장도 효율적으로 처리할 수 있다는 장점이 있습니다. attention 구조의 등장으로 기계 번역 모델의 성능이 크게 향상되었지만, RNN 모델 자체의 한계점은 여전히 문제는 남아있었는데요. (여러 가지 개선 방법들이 제안되었음에도 남아있는) long-term dependency 문제와 gradient vanishing/explosion 문제, 오래 학습해야 한다는 점, 그리고 source sentence를 순서대로 입력받아야 하기 때문에 병렬처리가 어렵다는 점입니다. 이를 근본적으로 해결한 구조가 바로 Attention is All You Need(2017)에서 제안된 transformer입니다.

Reference

• LSTM & GRU